
如图1,在直角梯形 中,AD//BC,
中,AD//BC, 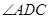 =900,BA="BC"
把ΔBAC沿
=900,BA="BC"
把ΔBAC沿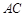 折起到
折起到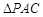 的位置,使得点
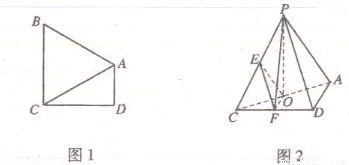
的位置,使得点 在平面ADC上的正投影O恰好落在线段
在平面ADC上的正投影O恰好落在线段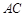 上,如图2所示,点
上,如图2所示,点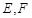 分别为线段PC,CD的中点.
分别为线段PC,CD的中点.
(I) 求证:平面OEF//平面APD;
(II)求直线CD 与平面POF
与平面POF
(III)在棱PC上是否存在一点 ,使得
,使得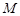 到点P,O,C,F四点的距离相等?请说明理由.
到点P,O,C,F四点的距离相等?请说明理由.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2013-2014学年山西省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
如图1,在直角梯形 中,
中,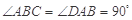 ,
,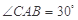 ,
,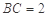 ,
,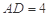 . 把
. 把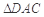 沿对角线
沿对角线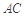 折起到
折起到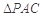 的位置,如图2所示,使得点
的位置,如图2所示,使得点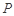 在平面
在平面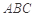 上的正投影
上的正投影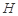 恰好落在线段
恰好落在线段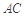 上,连接
上,连接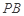 ,点
,点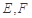 分别为线段
分别为线段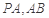 的中点.
的中点.
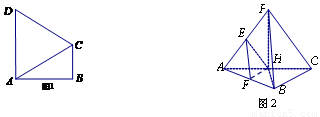
(1)求证:平面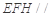 平面
平面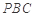 ;
;
(2)求直线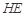 与平面
与平面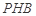 所成角的正弦值;
所成角的正弦值;
(3)在棱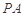 上是否存在一点
上是否存在一点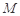 ,使得
,使得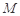 到点
到点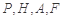 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区高三5月期末练习(二模)理科数学试卷(解析版) 题型:解答题
如图1,在直角梯形 中,
中, ,
, ,
,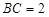 ,
,
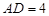 . 把
. 把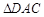 沿对角线
沿对角线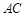 折起到
折起到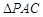 的位置,如图2所示,使得点
的位置,如图2所示,使得点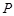 在平面
在平面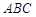 上的正投影
上的正投影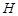 恰好落在线段
恰好落在线段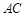 上,连接
上,连接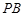 ,点
,点 分别为线段
分别为线段 的中点.
的中点.
(I)求证:平面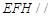 平面
平面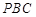 ;
;
(II)求直线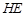 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)在棱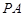 上是否存在一点
上是否存在一点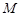 ,使得
,使得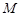 到点
到点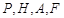 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三4月模拟理科数学试卷(解析版) 题型:解答题
如图1,
在直角梯形 中,
中,  ,
,  ,
, ,
, 为线段
为线段 的中点. 将
的中点. 将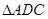 沿
沿 折起,使平面
折起,使平面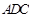
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(1)求证: 平面
平面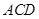 ;
;
(2)求二面角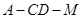 的余弦值.
的余弦值. 
查看答案和解析>>
科目:高中数学 来源:2014届广东省汕头市高二下学期期中文科数学试卷(解析版) 题型:解答题
如图1,在直角梯形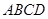 中,
中,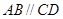 ,
, ,且
,且 .
.
现以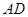 为一边向形外作正方形
为一边向形外作正方形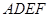 ,然后沿边
,然后沿边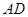 将正方形
将正方形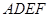 翻折,使平面
翻折,使平面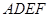 与平面
与平面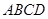 垂直,
垂直, 为
为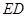 的中点,如图2.
的中点,如图2.
(1)求证: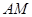 ∥平面
∥平面 ;
;
(2)求证: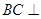 平面
平面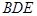 ;
;
(3)求点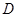 到平面
到平面 的距离.
的距离.
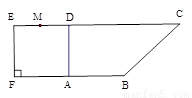

图 图
图
查看答案和解析>>
科目:高中数学 来源:2010年天津市天津一中高三下学期第五次月考数学(理) 题型:解答题
如图1,在直角梯形 中,
中,  ,
,
把△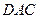 沿对角线
沿对角线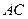 折起后如图2所示(点
折起后如图2所示(点 记为点
记为点 ), 点
), 点 在平面
在平面 上的正投影
上的正投影 落在线段
落在线段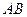 上, 连接
上, 连接 .
.
(1) 求直线 与平面
与平面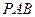 所成的角的大小;
所成的角的大小;
(2) 求二面角 的大小的余弦值.
的大小的余弦值.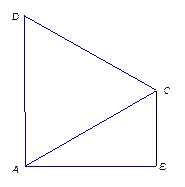

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com