
【题目】寒假即将到来,某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每在支出20元的各种费用(人工费,消耗费用等等).受市场调控,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的正整数倍)
(1)设宾馆一天的利润为W元, 求W与x的函数关系式;
(2)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
科目:高中数学 来源: 题型:
【题目】已知动点![]() 与两个定点
与两个定点![]() ,
,![]() 的距离的比为
的距离的比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最小值;
长度的最小值;
(3)已知圆![]() 的圆心为
的圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切,若圆
轴相切,若圆![]() 与曲线
与曲线![]() 有公共点,求实数
有公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1正方体![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在的直线进行翻折,将
所在的直线进行翻折,将![]() 沿
沿![]() 所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
所在直线进行翻折,在翻折的过程中,下列说法错误的是( )

A. 无论旋转到什么位置,![]() 、
、![]() 两点都不可能重合
两点都不可能重合
B. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
C. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
D. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 是椭圆
是椭圆![]() 上的任意一点,直线
上的任意一点,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率都存在.
的斜率都存在.

(1)若直线![]() 过原点,求证:
过原点,求证:![]() 为定值;
为定值;
(2)若直线![]() 不过原点,且
不过原点,且![]() ,试探究
,试探究![]() 是否为定值.
是否为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中, AC⊥BC,四边形ABED是正方形,平面ABED⊥平面ABC,点F,G,H分别为BD,EC,BE的中点,求证:
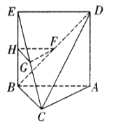
(1) BC⊥平面ACD
(2)平面HGF∥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种室内植物的株高![]() (单位:
(单位:![]() )与与一定范围内的温度
)与与一定范围内的温度![]() (单位:
(单位:![]() )有,现收集了该种植物的
)有,现收集了该种植物的![]() 组观测数据,得到如图所示的散点图:
组观测数据,得到如图所示的散点图:

现根据散点图利用![]() 或
或![]() 建立
建立![]() 关于
关于![]() 的回归方程,令
的回归方程,令![]() ,
,![]() ,得到如下数据:
,得到如下数据:
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
且![]() 与
与![]() 的相关系数分别为
的相关系数分别为![]() 、
、![]() ,其中
,其中![]() .
.
(1)用相关系数说明哪种模型建立![]() 关于
关于![]() 的回归方程更合适;
的回归方程更合适;
(2)(i)根据(1)的结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知这种植物的利润![]() (单位:千元)与
(单位:千元)与![]() 、
、![]() 的关系为
的关系为![]() ,当
,当![]() 何值时,利润的预报值最大.
何值时,利润的预报值最大.
附:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() ,
,
相关系数 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有车牌尾号为![]() 的汽车
的汽车![]() 和尾号为
和尾号为![]() 的汽车
的汽车![]() ,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日,
,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日, ![]() 车日出车频率
车日出车频率![]() ,
, ![]() 车日出车频率
车日出车频率![]() .该地区汽车限行规定如下:
.该地区汽车限行规定如下:
车尾号 |
|
|
|
|
|
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且![]() ,
, ![]() 两车出车相互独立.
两车出车相互独立.
(I)求该单位在星期一恰好出车一台的概率.
(II)设![]() 表示该单位在星期一与星期二两天的出车台数之和,求
表示该单位在星期一与星期二两天的出车台数之和,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是椭圆![]() 上的动点,
上的动点,![]() 、
、![]() 为椭圆的左、右焦点,O为坐标原点,若M是
为椭圆的左、右焦点,O为坐标原点,若M是![]() 的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
②已知![]() 为两个命题,若
为两个命题,若![]() 为假命题,则
为假命题,则![]() 为真命题;
为真命题;
③“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④“若![]() 则
则![]() 且
且![]() ”的逆否命题为真命题.
”的逆否命题为真命题.
其中 真命题的序号是__________.(写出所有满足题意的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com