
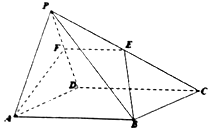
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.分析 (1)证明CD∥EF,AB∥CD,即可证明AB∥EF,利用线面平行的判定即可得解;
(2)利用平面PAD⊥平面ABCD,证明CD⊥AF,PA=AD,所以AF⊥PD,即可证明AF⊥平面PCD;
解答 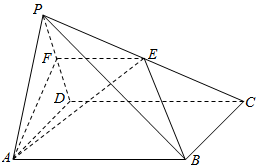 (本题满分为12分)
(本题满分为12分)
解:(1)证明:因为点E、F分别是棱PC和PD的中点,
所以CD∥EF.
因为底面ABCD是矩形,
所以AB∥CD.可得:AB∥EF,
又因为EF?平面PAB,AB?平面PAB,
所以EF∥平面PAB.…(6分)
(2)证明:在矩形ABCD中,CD⊥AD.
又因为平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
所以CD⊥平面PAD.
又AF?平面PAD,
所以CD⊥AF.
由点F是棱PD中点.
在△PAD中,因为PA=AD,所以AF⊥PD.
又因为PD∩CD=D,所以AF⊥平面PCD.…(12分)
点评 本题考查线面平行的性质,平面与平面垂直的性质,考查线面垂直,考查学生分析解决问题的能力,属于中档题.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{11}{3}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 实轴长相等 | B. | 离心率相等 | C. | 范围相同 | D. | 渐近线相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-2\sqrt{3}+\sqrt{5}}{6}$ | B. | $\frac{2\sqrt{3}+\sqrt{5}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{5}}{6}$ | D. | $\frac{-2\sqrt{3}-\sqrt{5}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20}{3}$ | B. | 8 | C. | $\frac{14}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com