
科目:高中数学 来源:2017届湖南长沙一中高三理月考五数学试卷(解析版) 题型:解答题
在等腰 中,
中, ,腰长为2,
,腰长为2, 、
、 分别是边
分别是边 、
、 的中点,将
的中点,将 沿
沿 翻折,得到四棱锥
翻折,得到四棱锥 ,且
,且 为棱
为棱 中点,
中点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面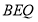 ?若存在,求二面角
?若存在,求二面角 的余弦值,若不存在,请说明理由.
的余弦值,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙雅礼中学高三文月考四数学试卷(解析版) 题型:解答题
如图,在三棱锥 中,
中, ,
, ,点
,点 为
为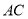 中点,
中点, 是
是 上一点,
上一点, 底面
底面 ,
, 面
面 .
.

(1)求证: 为
为 中点;
中点;
(2)当 取何值时,
取何值时,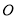 在平面
在平面 内的射影恰好是
内的射影恰好是 的中点.
的中点.
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙雅礼中学高三文月考四数学试卷(解析版) 题型:选择题
“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体. 它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣和(牟和)在一起的方形伞(方盖). 其直观图如下左图,图中四边形是为体现其直观性所作的辅助线. 其实际直观图中四边形不存在,当正视图和侧视图完全相同时,它的的正视图和俯视图分别可能是( )


A. B.
B.
C.  D.
D.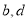
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二理上学期周检八数学试卷(解析版) 题型:选择题
定义区间 、
、 、
、 、
、 的长度均为
的长度均为 ,用
,用 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, .记
.记 ,设
,设 ,
, ,若用
,若用 表示不等式
表示不等式
 解集区间长度,则
解集区间长度,则 当时有( )
当时有( )
A. B.
B.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com