
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
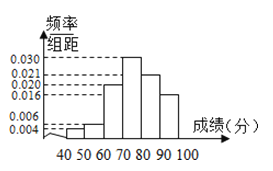
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
【答案】(1)众数是75,中位数约为76.7;(2)平均成绩约为74.
【解析】
试题(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求;由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.(2)样本平均值应是频率分布直方图的“重心”,即所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可.
试题解析:(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求,所以众数应为![]() .
.
由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.
∵![]() .
.
∴前三个小矩形面积的和为![]() ,而第四个小矩形面积为
,而第四个小矩形面积为![]() ,
,
∴中位数应位于第四个小矩形内.
设其底边为![]() ,高为
,高为![]() ,∴令
,∴令![]() 得
得![]() ,故中位数约为
,故中位数约为![]() .
.
(2)样本平均值应是频率粉绿分布直方图的“重心”,即所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可,
∴平均成绩为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与直线
的直线与直线![]() 相交于点
相交于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率
的离心率![]() ;
;
(2)![]() 是圆
是圆![]() :
:![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某高中随机抽取部分高二学生,调査其到校所需的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中到校所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)如果学生到校所需时间不少于1小时,则可申请在学校住宿.若该校录取1200名新生,请估计高二新生中有多少人可以申请住宿;
(3)以直方图中的频率作为概率,现从该学校的高二新生中任选4名学生,用![]() 表示所选4名学生中“到校所需时间少于40分钟”的人数,求
表示所选4名学生中“到校所需时间少于40分钟”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为 ![]() ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为 ![]() ,已知该厂三个生产小组分别每月负责生产一台这种仪器.
,已知该厂三个生产小组分别每月负责生产一台这种仪器.
(1)求本月恰有两台仪器完全合格的概率;
(2)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为ξ,求ξ的分布列和每月的盈利期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2+bx(a为实常数).
(1)若a=﹣2,b=﹣3,求f(x)的单调区间;
(2)若b=0,且a>﹣2e2 , 求函数f(x)在[1,e]上的最小值及相应的x值;
(3)设b=0,若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
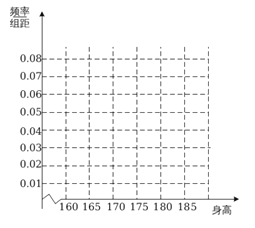
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,且圆心在直线
,且圆心在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点,问在直线
两点,问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出点
恒成立?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com