
【题目】已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,其外接圆为圆H.
,其外接圆为圆H.
![]() 求圆H的标准方程;
求圆H的标准方程;
![]() 若直线l过点C,且被圆H截得的弦长为2,求直线l的方程.
若直线l过点C,且被圆H截得的弦长为2,求直线l的方程.
【答案】(1)![]() ; (2)
; (2)![]() 或
或![]() .
.
【解析】
![]() 根据题意,由三点的坐标求出直线AB、BC的垂直平分线,联立直线的方程即可得圆心的坐标,进而求出圆的半径,计算可得答案;
根据题意,由三点的坐标求出直线AB、BC的垂直平分线,联立直线的方程即可得圆心的坐标,进而求出圆的半径,计算可得答案;
![]() 根据题意,由直线与圆的位置关系,求出圆心到直线的距离,分直线的斜率存在与不存在两种情况讨论,求出直线的方程,综合可得答案.
根据题意,由直线与圆的位置关系,求出圆心到直线的距离,分直线的斜率存在与不存在两种情况讨论,求出直线的方程,综合可得答案.
![]() 根据题意,
根据题意,![]() ,
,![]() ,
,![]() ,
,
则AB的垂直平分线是![]() ,
,
又由![]() ,
,![]() ,则BC的方程为
,则BC的方程为![]() ,BC中点是
,BC中点是![]() ,
,
则BC的垂直平分线是![]() ,
,
联立![]() ,解可得
,解可得![]() ,即圆心H的坐标为
,即圆心H的坐标为![]() ,
,
又由![]() ,
,
则圆H的方程为![]() ;
;
![]() 根据题意,若直线l被圆H截得的弦长为2,则圆心H到直线的距离
根据题意,若直线l被圆H截得的弦长为2,则圆心H到直线的距离![]() ,
,
若直线l的斜率不存在,直线l的方程为![]() ,符合题意;
,符合题意;
若直线l的斜率存在,设其方程为![]() ,
,
有![]() ,解可得
,解可得![]() ,
,
则直线l的方程为![]() ,即
,即![]() ,
,
则直线l的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
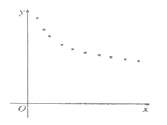
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为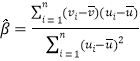 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(-1,3),点C(4,-2),且其“欧拉线”与圆M:![]() 相切,则下列结论正确的是( )
相切,则下列结论正确的是( )
A.圆M上点到直线![]() 的最小距离为2
的最小距离为2![]()
B.圆M上点到直线![]() 的最大距离为3
的最大距离为3![]()
C.若点(x,y)在圆M上,则![]() 的最小值是
的最小值是![]()
D.圆![]() 与圆M有公共点,则a的取值范围是
与圆M有公共点,则a的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国际海洋安全规定:两国军舰正常状况下(联合军演除外),在公海上的安全距离为20![]() (即距离不得小于20
(即距离不得小于20![]() ),否则违反了国际海洋安全规定.如图,在某公海区域有两条相交成60°的直航线
),否则违反了国际海洋安全规定.如图,在某公海区域有两条相交成60°的直航线![]() ,
,![]() ,交点是
,交点是![]() ,现有两国的军舰甲,乙分别在
,现有两国的军舰甲,乙分别在![]() ,
,![]() 上的
上的![]() ,
,![]() 处,起初
处,起初![]() ,
,![]() ,后来军舰甲沿
,后来军舰甲沿![]() 的方向,乙军舰沿
的方向,乙军舰沿![]() 的方向,同时以40
的方向,同时以40![]() 的速度航行.
的速度航行.
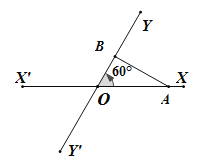
(1)起初两军舰的距离为多少?
(2)试判断这两艘军舰是否会违反国际海洋安全规定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应德智体美劳的教育方针,唐徕回中高一年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下:
每分钟跳绳个数 |
|
|
|
| 185以上 |
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了了解学生的体质,随机抽取了100名学生,统计了他的跳绳个数,并绘制了如下样本频率直方图:
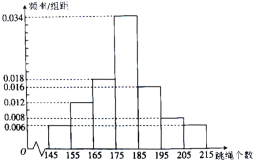
(1)现从这100名学生中,任意抽取2人,求两人得分之和小于35分的概率(结果用最简分数表示);
(2)若该校高二年级2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
①估计每分钟跳绳164个以上的人数(四舍五入到整数)
②若在全年级所有学生中随机抽取3人,记每分钟跳绳在179个以上的人数为![]() ,求
,求![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
(若随机变量![]() 服从正态分布
服从正态分布![]() 则
则![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AD.M,N分别是AB,PC的中点.
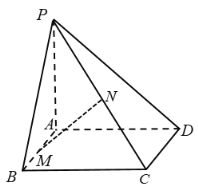
(1)求证:MN//平面PAD;
(2)求证:MN⊥平面PCD;
(3)求二面角B—PC—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )
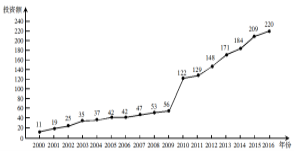
A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com