
【题目】在某海礁A处有一风暴中心,距离风暴中心A正东方向200km的B处有一艘轮船,正以北偏西a(a为锐角)角方向航行,速度为40km/h.已知距离风暴中心180km以内的水域受其影响.
(1)若轮船不被风暴影响,求角α的正切值的最大值?
(2)若轮船航行方向为北偏西45°,求轮船被风暴影响持续多少时间?
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN= ![]() BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF﹣CB,M为EF中点.
BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF﹣CB,M为EF中点. 
(1)求证:平面A′MN⊥平面A′BF;
(2)求二面角E﹣A′F﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为棱AB,BC的中点,点F在侧棱B1B上,且B1E⊥C1F,A1C1⊥B1C1.
(1)求证:DE∥平面A1C1F;
(2)求证:B1E⊥平面A1C1F

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若点![]() 是
是![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() :
:![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
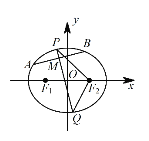
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com