
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1) 求导函数,对其进行因式分解,对![]() 分成
分成![]() ,
,![]() ,
,![]() ,
,![]() 几类进行讨论,从而可确定函数
几类进行讨论,从而可确定函数![]() 的单调性与单调区间;
的单调性与单调区间;
(2) 对![]() 分成
分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 几类,利用函数的单调性和零点存在性定理,由
几类,利用函数的单调性和零点存在性定理,由![]() 在
在![]() 上有且只有一个零点,求解参数范围.
上有且只有一个零点,求解参数范围.
解:(1)定义域为![]() ,
,![]() ,
,
(Ⅰ)当![]() 时,
时,![]() ;
;![]() ,
,
即![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增;
上单调递增;
(Ⅱ)当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ,
,
(i)若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
(ii)若![]() ,则
,则![]() ,
,![]() 或
或![]() ;
;![]() ,
,
即![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减,
上单调递减,
(iii)若![]() ,则
,则![]() 或
或![]() ;
;![]() ,
,
即![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减.
上单调递减.
(2)(Ⅰ)当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上有两个零点;
上有两个零点;
(Ⅱ)当![]() 时,
时,![]() ,令
,令![]() 得
得![]() ,又知当
,又知当![]() 时
时![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上有且只有一个零点;
上有且只有一个零点;
(Ⅲ)当![]() 时,
时,
(i)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
此时![]() 在
在![]() 上有且只有一个零点;
上有且只有一个零点;
(ii)当![]() 时,由(1)结合
时,由(1)结合![]() 的单调性
的单调性![]() ,只需讨论
,只需讨论![]() 的符号,
的符号,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上有且只有一个零点;
上有且只有一个零点;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上无零点;
上无零点;
(iii)若![]() 由(1)结合
由(1)结合![]() 的单调性,
的单调性,![]() ,
,![]() ,此时
,此时![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
综上所述,![]() .
.


科目:高中数学 来源: 题型:
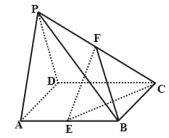
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 为正三角形,且面
为正三角形,且面![]() 面
面![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)(文科)求三棱锥![]() 的体积;
的体积;
(理科)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 经过点
经过点![]() ,且离心率
,且离心率![]() .
.
(1)求椭圆E的方程;
(2)设椭圆E的右顶点为A,若直线![]() 与椭圆E相交于MN两点(异于A点),且满足
与椭圆E相交于MN两点(异于A点),且满足![]() ,试证明直线l经过定点,并求出该定点的坐标.
,试证明直线l经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法自古以来就使用的纪年方法,甲、乙、丙、丁、戊、已、庚、辛、壬、癸为十天干;子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥为十二地支.“干支纪年法”是以一个天干和一个地支按上述顺序相配排列起来,天干在前,地支在后,已知2017年是丁酉年,2018年是戊戌年,2019年是已亥年,依此类推,则2080年是____________年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() ,抛物线的通径与椭圆的右通径在同一直线上.
,抛物线的通径与椭圆的右通径在同一直线上.
(1)求椭圆与抛物线的标准方程;
(2)过抛物线焦点且倾斜角为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点,
两点,![]() 为椭圆的左焦点,求
为椭圆的左焦点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶某村![]() 户贫困户.为了做到精准帮扶,工作组对这
户贫困户.为了做到精准帮扶,工作组对这![]() 户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标
户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() .将指标
.将指标![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,得到如图所示的频率分布直方图.规定若
分成五组,得到如图所示的频率分布直方图.规定若![]() ,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当
,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当![]() 时,认定该户为“亟待帮住户”.工作组又对这
时,认定该户为“亟待帮住户”.工作组又对这![]() 户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.
户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.

(1)完成下面的列联表,并判断是否有![]() 的把握认为绝对贫困户数与受教育水平不好有关:
的把握认为绝对贫困户数与受教育水平不好有关:
受教育水平良好 | 受教育水平不好 | 总计 | |
绝对贫困户 |
| ||
相对贫困户 |
| ||
总计 |
|
(2)上级部门为了调查这个村的特困户分布情况,在贫困指标处于![]() 的贫困户中,随机选取两户,用
的贫困户中,随机选取两户,用![]() 表示所选两户中“亟待帮助户”的户数,求
表示所选两户中“亟待帮助户”的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附: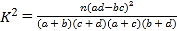 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15∽65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
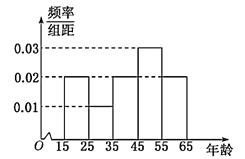
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com