
(03年北京卷文)(15分)
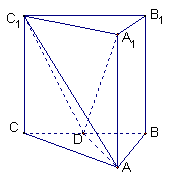
如图,正三棱柱ABC―A1B1C1中,D是BC的中点,AB=a.
(Ⅰ)求证:直线A1D⊥B1C1;
(Ⅱ)求点D到平面ACC1的距离;
(Ⅲ)判断A1B与平面ADC的位置关系,
并证明你的结论.
解析:(Ⅰ)证法一:∵点D是正△ABC中BC边的中点,∴AD⊥BC,
又A1A⊥底面ABC,∴A1D⊥BC ,∵BC∥B1C1,∴A1D⊥B1C1.
证法二:连结A1C1,则A1C=A1B. ∵点D是正△A1CB的底边中BC的中点,
∴A1D⊥BC ,∵BC∥B1C1,∴A1D⊥B1C1.
(Ⅱ)解法一:作DE⊥AC于E, ∵平面ACC1⊥平面ABC,
∴DE⊥平面ACC1于E,即DE的长为点D到平面ACC1的
距离. 在Rt△ADC中,AC=2CD=![]()
∴所求的距离![]()

解法二:设点D到平面ACC1的距离为![]() ,
,
∵体积![]()
![]()
![]() 即点D到平面ACC1的距离为
即点D到平面ACC1的距离为![]() .
.
(Ⅲ)答:直线A1B//平面ADC1,证明如下:
证法一:如图1,连结A1C交AC1于F,则F为A1C的中点,∵D是BC的中点,∴DF∥A1B,
又DF![]() 平面ADC1,A1B
平面ADC1,A1B![]() 平面ADC1,∴A1B∥平面ADC1.
平面ADC1,∴A1B∥平面ADC1.
证法二:如图2,取C1B1的中点D1,则AD∥A1D1,C1D∥D1B,
∴AD∥平面A1D1B,且C1D∥平面A1D1B,
∴平面ADC1∥平面A1D1B,∵A1B![]() 平面A1D1B,∴A1B∥平面ADC1.
平面A1D1B,∴A1B∥平面ADC1.



 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
(03年北京卷文)(12分)
如图,ABCD―A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点.
(Ⅰ)求三棱锥D1―DBC的体积.;
(Ⅱ)证明BD1∥平面C1DE;
(Ⅲ)求面C1DE与面CDE所成二面角的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
(03年北京卷文)(15分)
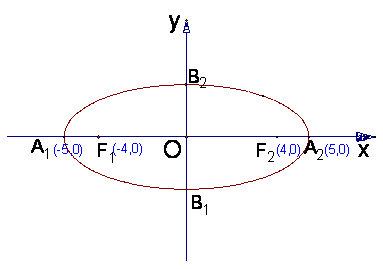
如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.
(Ⅰ)写出椭圆的方程及准线方程;
(Ⅱ)过线段OA上异于O,A的任一点K作OA的垂线,交椭圆于P,P1两点,直线
A1P与AP1交于点M.
求证:点M在双曲线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com