
分析 先根据角α终边上一点P确定tanα的值,进而利用诱导公式对原式进行化简整理后,把tanα的值代入即可.
解答 解:∵角α终边上一点P(-4,3),
∴tanα=$\frac{y}{x}$=-$\frac{3}{4}$,
∴$\frac{{sin(α-2π)+cos(\frac{π}{2}+α)sin(-π-α)}}{{cos(π-α)+cos(\frac{11π}{2}-α)sin(\frac{3π}{2}+α)}}$=$\frac{sinα-si{n}^{2}α}{-cosα(1-sinα)}$=-tanα=$\frac{3}{4}$.
点评 本题主要考查了运用诱导公式化简求值的问题.要特别留意在三角函数转换过程中三角函数的正负号的判定,属于基础题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 4 | C. | -1或4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
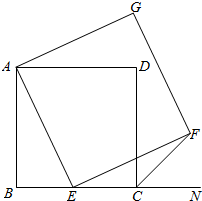 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-∞,0) | C. | (-1,0) | D. | [-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com