
���� ��1��ֱ�Ӹ�����Բ�Ķ�������a��������a2=b2+c2���c���ɣ�
��2����������������Τ�ﶨ�����x1+x2=$-\frac{4t}{3}$��y1+y2=x1+x2+2t=$\frac{2t}{3}$�������е����굽Բ���̼������tֵ��
��� �⣺��1����ΪF1��F2Ϊ���ҽ��㣬P����Բ������һ�㣬��|PF1|+|PF2|=2$\sqrt{2}$
��a=$\sqrt{2}$��
��2c=2⇒c=1��
��b=$\sqrt{{a}^{2}-{c}^{2}}$=1��
���ԣ���Բ����Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}=1$
��2����A��x1��y1����B��x2��y2��
����������$\left\{\begin{array}{l}{x-y+t=0}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$��������У�3x2+4tx+2t2-2=0 �٣�
�ɢ�֪��x1+x2=$-\frac{4t}{3}$
���ԣ�y1+y2=x1+x2+2t=$\frac{2t}{3}$��
�����߶�AB���е���Բx2+y2=$\frac{5}{6}$�ϣ�
�����У�$��-\frac{2t}{3}��^{2}+��\frac{t}{3}��^{2}=\frac{5}{6}$⇒t=��$\frac{\sqrt{6}}{2}$�����ᣩ��
�ʴ���t=$\frac{\sqrt{6}}{2}$��������
���� ������Ҫ��������Բ���̻������壬�Լ�Τ�ﶨ������Բ��ֱ���ۺ��е�Ӧ�ã����е��⣮


 ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{12}{5}$ | B�� | -$\frac{12}{5}$ | C�� | $\frac{5}{12}$ | D�� | -$\frac{5}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -9 | B�� | -1 | C�� | 1 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{7}$ | B�� | $\frac{3}{7}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -i | B�� | -1 | C�� | i | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
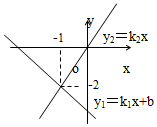 ��ͼ��ʾ��������y1=k1x+b��y2=k2x��ͼ���ཻ�ڵ㣨-1��-2���������x�IJ���ʽ k1x+b��k2x�Ľ⼯Ϊ��������
��ͼ��ʾ��������y1=k1x+b��y2=k2x��ͼ���ཻ�ڵ㣨-1��-2���������x�IJ���ʽ k1x+b��k2x�Ľ⼯Ϊ��������| A�� | x��-1 | B�� | x��-1 | C�� | x��-2 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com