(1)因为f(x)=ax+xlnx,所以f'(x)=a+lnx+1.(1分)
因为函数f(x)=ax+xlnx的图象在点x=e处的切线斜率为3,
所以f'(e)=3,即a+lne+1=3.所以a=1.(2分)
(2)解:由(1)知,f(x)=x+xlnx,
所以
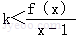
对任意x>1恒成立,即
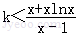
对任意x>1恒成立.(3分)
令
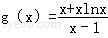
,则
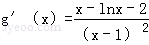
,(4分)
令h(x)=x﹣lnx﹣2(x>1),则
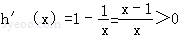
,
所以函数h(x)在(1,+∞)上单调递增.(5分)
因为h(3)=1﹣ln3<0,h(4)=2﹣2ln2>0,
所以方程h(x)=0在(1,+∞)上存在唯一实根x
0,且满足x
0∈(3,4).
当1<x<x
0时,h(x)<0,即g'(x)<0,当x>x
0时,h(x)>0,即g'(x)>0,
所以函数
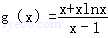
在(1,x
0)上单调递减,在(x
0,+∞)上单调递增.

.(7分)
所以k<[g(x)]
min=x
0∈(3,4).故整数k的最大值是3.(8分)
(3)证明:由(2)知,
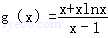
是[4,+∞)上的增函数,(9分)
所以当n>m≥4时,
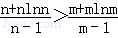
.(10分)
即n(m﹣1)(1+lnn)>m(n﹣1)(1+lnm).
整理,得mnlnn+mlnm>mnlnm+nlnn+(n﹣m).(11分)
因为n>m,所以mnlnn+mlnm>mnlnm+nlnn.(12分)
即lnn
mn+lnm
m>lnm
mn+lnn
n.
即ln(n
mnm
m)>ln(m
mnn
n).(13分)
所以(mn
n)
m>(nm
m)
n.(14分)
证明2:构造函数f(x)=mxlnx+mlnm﹣mxlnm﹣xlnx,(9分)
则f'(x)=(m﹣1)lnx+m﹣1﹣mlnm.(10分)
因为x>m≥4,所以f'(x)>(m﹣1)lnm+m﹣1﹣mlnm=m﹣1﹣lnm>0.
所以函数f(x)在[m,+∞)上单调递增.(11分)
因为n>m,所以f(n)>f(m).
所以mnlnn+mlnm﹣mnlnm﹣nlnn>m
2lnm+mlnm﹣m
2lnm﹣mlnm=0.(12分)
即mnlnn+mlnm>mnlnm+nlnn.
即lnn
mn+lnm
m>lnm
mn+lnn
n.
即ln(n
mnm
m)>ln(m
mnn
n).(13分)
所以(mn
n)
m>(nm
m)
n.

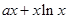 的图像在点
的图像在点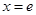 (
(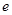 为自然常数)处的切线斜率为3.
为自然常数)处的切线斜率为3.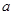 的值
的值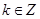 ,且
,且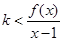 对任意的
对任意的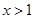 恒成立,求
恒成立,求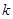 得最大值
得最大值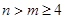 时,证明
时,证明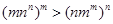
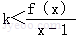 对任意x>1恒成立,即
对任意x>1恒成立,即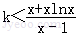 对任意x>1恒成立.(3分)
对任意x>1恒成立.(3分)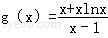 ,则
,则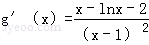 ,(4分)
,(4分)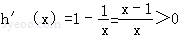 ,
,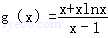 在(1,x0)上单调递减,在(x0,+∞)上单调递增.
在(1,x0)上单调递减,在(x0,+∞)上单调递增. .(7分)
.(7分)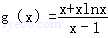 是[4,+∞)上的增函数,(9分)
是[4,+∞)上的增函数,(9分)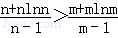 .(10分)
.(10分)

 名校课堂系列答案
名校课堂系列答案