
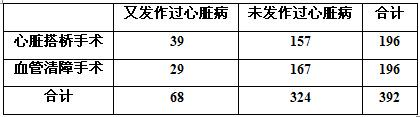
 对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如表所示:
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如表所示:| n(ac-bd)2 |
| (a+b)(d+c)(c+a)(b+d) |
| 392×(39×167-29×157)2 |
| 68×324×196×196 |
| n(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |


科目:高中数学 来源: 题型:
| 又发作过心脏病 | 未发作心脏病 | 合计 |
心脏搭桥手术 | 39 | 157 | 196 |
血管清障手术 | 29 | 167 | 196 |
合计 | 68 | 324 | 392 |
试根据上述数据比较这两种手术对病人又发作心脏病的影响有没有差别.
查看答案和解析>>
科目:高中数学 来源: 题型:
| 又发作过心脏病 | 未发作心脏病 | 合计 |
心脏搭桥手术 | 39 | 157 | 196 |
血管清障手术 | 29 | 167 | 196 |
合计 | 68 | 324 | 392 |
试根据上述数据比较这两种手术对病人又发作过心脏病有没有关系.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学变量间的相关关系、统计案例专项训练(河北) 题型:填空题
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:
|
|
又发作过心脏病 |
未发作过心脏病 |
合计 |
|
心脏搭桥手术 |
39 |
157 |
196 |
|
血管清障手术 |
29 |
167 |
196 |
|
合计 |
68 |
324 |
392 |
试根据上述数据计算K2=________;
比较这两种手术对病人又发作心脏病的影响有没有差别______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
| 又发作过心脏病 | 未发作心脏病 | 合计 |
心脏搭桥手术 | 39 | 157 | 196 |
血管清障手术 | 29 | 167 | 196 |
合计 | 68 | 324 | 392 |
试根据上述数据比较这两种手术对病人又发作心脏病的影响有没有差别.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com