
【题目】己知某区甲、乙、丙三所学校的教师志愿者人数分别为240,160,80.为助力疫情防控,现采用分层抽样的方法,从这三所学校的教师志愿者中抽取6名教师,参与“抗击疫情·你我同行”下卡口执勤值守专项行动.
(Ⅰ)求应从甲、乙、丙三所学校的教师志愿者中分别抽取的人数;
(Ⅱ)设抽出的6名教师志愿者分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,现从中随机抽取2名教师志愿者承担测试体温工作.
,现从中随机抽取2名教师志愿者承担测试体温工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2名教师志愿者来自同一所学校”,求事件
为事件“抽取的2名教师志愿者来自同一所学校”,求事件![]() 发生的概率.
发生的概率.
【答案】(Ⅰ)3人,2人,1人;(Ⅱ)(i)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(ⅱ)
;(ⅱ)![]()
【解析】
(Ⅰ)按照分层抽样规则计算可得;
(Ⅱ)(i)将所有可能结果一一列举,做到不重复不遗漏;
(ii)根据古典概型的概率公式计算可得;
解:(Ⅰ)由已知,甲、乙、丙三所学校的教师志愿者人数之比为3:2:1
由于采用分层抽样的方法从中抽取6名教师,因此应从甲、乙、丙三所学校的教师志愿者中分别抽取3人,2人,1人.
(Ⅱ)(ⅰ)从抽出的 名教师中随机抽取2名教师的所有可能结果为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种.
,共15种.
(ⅱ)由(Ⅰ),不妨设抽出的6名教师中,来自甲学校的是![]() ,
,![]() ,
,![]() ,来自乙学校的是
,来自乙学校的是![]() ,
,![]() ,来自丙学校的是
,来自丙学校的是![]() ,则从抽出的6名教师中随机抽取的2名教师来自同一学校的所有可能结果为
,则从抽出的6名教师中随机抽取的2名教师来自同一学校的所有可能结果为![]() ,
,![]() ,
,![]() ,
,![]() ,共4种.
,共4种.
所以,事件![]() 发生的概率
发生的概率![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图是一个几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() 为全等的等边三角形,
为全等的等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,在此几何体中,下列结论中正确的个数有()
的中点,在此几何体中,下列结论中正确的个数有()
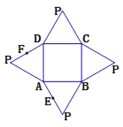
①平面![]() 平面
平面![]()
②直线![]() 与直线
与直线![]() 是异面直线
是异面直线
③直线![]() 与直线
与直线![]() 共面
共面
④面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷![]() 广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元
广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元![]() 不足1小时的部分按1小时计算
不足1小时的部分按1小时计算![]() 甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为
甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为![]() ;一小时以上且不超过两小时还车的概率分别为
;一小时以上且不超过两小时还车的概率分别为![]() ;两人租车时间都不会超过三小时.
;两人租车时间都不会超过三小时.
![]() Ⅰ
Ⅰ![]() 求甲、乙两人所付租车费用相同的概率;
求甲、乙两人所付租车费用相同的概率;
![]() Ⅱ
Ⅱ![]() 设甲、乙两人所付的租车费用之和为随机变量
设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E﹣BCD的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种商品的经验表明,该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() 为常数.已知销售价格为5元/千克时,每日可售出该商品13千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品13千克.
(1)求![]() 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大,并求出最大利润.
的值,使商场每日销售该商品所获得的利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当![]() 时,若函数
时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当![]() 时,若
时,若![]() 的解集为
的解集为![]() ,且
,且![]() 中有且仅有一个整数,求实数
中有且仅有一个整数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
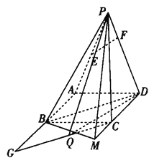
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,求
的中点,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com