
【题目】在边长为2的正方体ABCD﹣A1B1C1D1中,E是BC的中点,F是DD1的中点,
(1)求点A到平面A1DE的距离;
(2)求证:CF∥平面A1DE;
(3)求二面角E﹣A1D﹣A的平面角大小的余弦值.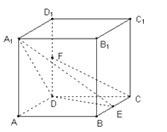
【答案】解:(1)分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角坐标系,则A(2,0,0),A1(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),
∴![]() =(2,0,2),
=(2,0,2),![]() =(1,2,0),
=(1,2,0),![]() =(2,0,0)
=(2,0,0)
设平面A1DE的法向量是![]() =(a,b,c)
=(a,b,c)
则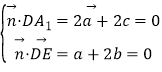 ,∴
,∴![]() =(﹣2,1,2)
=(﹣2,1,2)
∴点A到平面A1DE的距离是d=![]() =
=![]() ;
;
(2)证明:∵![]() =(0,﹣2,1),
=(0,﹣2,1),
∴![]()
![]() =﹣2+2=0,∴
=﹣2+2=0,∴![]() ⊥
⊥![]() ,
,
∴CF∥平面A1DE;
(3)解:∵平面A1DA的法向量为![]() =(0,2,0),平面A1DE的法向量是
=(0,2,0),平面A1DE的法向量是![]() =(﹣2,1,2)
=(﹣2,1,2)
∴cos<![]() ,
,![]() >=
>=![]() =
=![]() =
=![]() .
.
【解析】(1)分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角坐标系,利用向量的点到平面的距离公式即可求得点A到平面A1DE的距离;
(2)确定![]()
![]() =﹣2+2=0,可得
=﹣2+2=0,可得![]() ⊥
⊥![]() , 从而可得CF∥平面A1DE;
, 从而可得CF∥平面A1DE;
(3)确定平面A1DA的法向量、平面A1DE的法向量,利用向量的夹角公式,即可得到结论.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
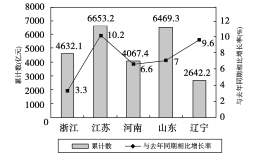
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形ABCD中, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3). 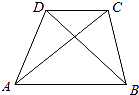
(1)若 ![]() ∥
∥ ![]() ,求x与y满足的关系式;
,求x与y满足的关系式;
(2)满足(1)的同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值.
,求x,y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾天气对城市环境造成很大影响,按照国家环保部发布的标准:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米.某市环保部门加强了对空气质量的监测,抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据,制成茎叶图,如图:
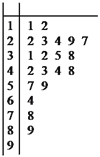
(Ⅰ)完成如下频率分布表,并在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
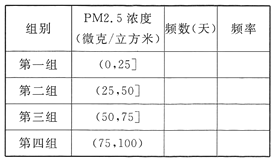
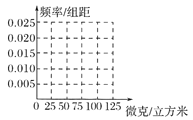
(Ⅱ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在正项等比数列{an}中,a1=1,a2a4=16,则|a1﹣12|+|a2﹣12|+…+|a8﹣12|=( )
A.224
B.225
C.226
D.256
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:
(1)当a,b均为整数时;
(2)当a,b均为实数时.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)= ![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①f(﹣x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(﹣1,1);
③若x1≠x2 , 则一定有f(x1)≠f(x2);
④函数g(x)=f(x)﹣x在R上有三个零点.
其中正确结论的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边分别是a、b、c,已知B=60°,
(1)若b= ![]() ,A=45°,求a;
,A=45°,求a;
(2)若a、b、c成等比数列,请判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com