
【题目】如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且![]() ,
,![]() .
.
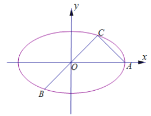
(Ⅰ)求椭圆E的方程;
(Ⅱ)设![]() 是以原点为圆心,短轴长为半径的圆,过椭圆E上异于其顶点的任一点P,作
是以原点为圆心,短轴长为半径的圆,过椭圆E上异于其顶点的任一点P,作![]() 的两条切线,切点分别为M,N,若直线MN在x轴、y轴上的截距分别为m,n,试计算
的两条切线,切点分别为M,N,若直线MN在x轴、y轴上的截距分别为m,n,试计算![]() 的值是否为定值?如果是,请给予证明;如果不是,请说明理由.
的值是否为定值?如果是,请给予证明;如果不是,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)是定值,证明见解析.
;(Ⅱ)是定值,证明见解析.
【解析】
(Ⅰ)由已知得![]() ,数形结合求得
,数形结合求得![]() 的坐标,代入椭圆方程求得
的坐标,代入椭圆方程求得![]() ,则椭圆方程可求;
,则椭圆方程可求;
(Ⅱ)设![]() ,
,![]() ,由
,由![]() ,
,![]() 是切点,可知
是切点,可知![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.分别写出以
四点共圆.分别写出以![]() 为直径的圆的方程与圆
为直径的圆的方程与圆![]() 的方程,联立可得
的方程,联立可得![]() 所在直线方程求出直线
所在直线方程求出直线![]() 在
在![]() ,
,![]() 轴上的截距,结合
轴上的截距,结合![]() 在椭圆上可得
在椭圆上可得![]() 的值是定值.
的值是定值.
解:(Ⅰ)依题意知:椭圆的长半轴长![]() ,则
,则![]() ,
,
设椭圆![]() 的方程为
的方程为![]()
由椭圆的对称性知![]() ,又
,又![]()
![]()
![]() ,
,![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() 点C的坐标为
点C的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,
将C的坐标![]() 代入椭圆方程得
代入椭圆方程得![]()
![]() 所求的椭圆
所求的椭圆![]() 的方程为
的方程为![]()
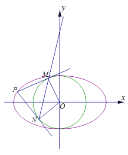
(Ⅱ)设点![]() ,由
,由![]() ,
,![]() 是
是![]() 的切点知,
的切点知,![]() ,
,![]() ,
,
![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一圆上,
四点在同一圆上,
且圆的直径为OP则圆心为![]() ,
,
其方程为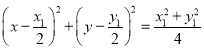 ,
,
即![]() ①
①
即点![]() ,
,![]() 满足方程①,又点
满足方程①,又点![]() ,
,![]() 都在
都在![]() 上,
上,
![]() ,
, ![]() 坐标也满足方程
坐标也满足方程![]() ②
②
②![]() ①得直线
①得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() 得
得![]() ,
,
![]() ,
,![]() ,又点Р在椭圆E上,
,又点Р在椭圆E上,
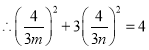 ,即
,即![]() 为定值.
为定值.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点,给出命题:①
的零点,给出命题:①![]() ;②若
;②若![]() ,则存在
,则存在![]() ,使得
,使得![]() ;③
;③![]() 与
与![]() 所有极值之和一定小于0;④若
所有极值之和一定小于0;④若![]() ,且
,且![]() 是曲线
是曲线![]() 的一条切线,则
的一条切线,则![]() 的取值范围是
的取值范围是![]() .则以上命题正确序号是_____________.
.则以上命题正确序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知A,B分别为椭圆C:![]() (a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,
(a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,![]()
![]() =﹣4,△PAB的面积的最大值为
=﹣4,△PAB的面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)若椭圆C上存在两点M,N,分别满足OM∥PA,ON∥PB,求|OM||ON|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”.
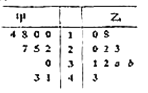
(Ⅰ)求在这10个卖场中,甲型号汽车的“星级卖场”的个数;
(Ⅱ)若在这10个卖场中,乙型号汽车销售量的平均数为26.7,求![]() 的概率;
的概率;
(Ⅲ)若![]() ,记乙型号汽车销售量的方差为
,记乙型号汽车销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值(只写出结论).
达到最小值(只写出结论).
注:方差![]() ,其中
,其中![]() 是
是![]() ,
,![]() ,…,
,…,![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线l与椭圆C交于P,Q两点,且点M满足
,直线l与椭圆C交于P,Q两点,且点M满足![]() .
.
(1)若点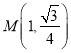 ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线l过点![]() 且不与x轴重合,过点M作垂直于l的直线
且不与x轴重合,过点M作垂直于l的直线![]() 与y轴交于点
与y轴交于点![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的单调性;
的单调性;
(2)若![]() ,对于任意
,对于任意![]() ,是否存在与
,是否存在与![]() 有关的正常数
有关的正常数![]() ,使得
,使得![]() 成立?如果存在,求出一个符合条件的
成立?如果存在,求出一个符合条件的![]() ;否则说明理由.
;否则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com