
已知 是实数,函数
是实数,函数 .
.
⑴求函数f(x)的单调区间;
⑵设g(x)为f(x)在区间 上的最小值.
上的最小值.
(i)写出g(a)的表达式;(ii)求 的取值范围,使得
的取值范围,使得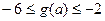 .
.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 .
.
(Ⅰ)若 为
为 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若 在
在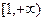 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)若 时,方程
时,方程 有实根,求实数
有实根,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.
(I)当 时,求函数
时,求函数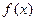 的单调
的单调 递增区间;
递增区间;
(II)设|MN|= ,试求函数
,试求函数 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数 ,在区间
,在区间 内,总存在m+1个数
内,总存在m+1个数 使得不等式
使得不等式 成立,求m的最大值.
成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某汽车销售公司在A、B两地销售同一种品牌的汽车,在A地的销售利润(单位:万元)为y1=4.1x-0.1x2,在B地的销售利润(单位:万元)为y2=2x,其中x为销售量(单位:辆).若该公司在两地共销售16辆这种品牌汽车,则能获得的最大利润是( )
A.10.5万元 B.11万元 C.43万元 D.43.025万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com