
【题目】一款手游,页面上有一系列的伪装,其中隐藏了4个宝藏.如果你在规定的时间内找到了这4个宝藏,将会弹出下一个页面,这个页面仍隐藏了2个宝藏,若能在规定的时间内找到这2个宝藏,那么闯关成功,否则闯关失败,结束游戏;如果你在规定的时间内找到了3个宝藏,仍会弹出下一个页面,但这个页面隐藏了4个宝藏,若能在规定的时间内找到这4个宝藏,那么闯关成功,否则闯关失败,结束游戏;其它情况下,不会弹出下一个页面,闯关失败,并结束游戏.
假定你找到任何一个宝藏的概率为![]() ,且能否找到其它宝藏相互独立..
,且能否找到其它宝藏相互独立..
(1)求闯关成功的概率;
(2)假定你付1个Q币游戏才能开始,能进入下一个页面就能获得2个Q币的奖励,闯关成功还能获得另外4个Q币的奖励,闯关失败没有额外的奖励.求一局游戏结束,收益的Q币个数X的数学期望(收益=收入-支出).
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
![]() 函数在
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 点
点![]() 是函数图象的一个对称中心;
是函数图象的一个对称中心;
![]() 函数图象关于直线
函数图象关于直线![]() 对称;
对称;
![]() 存在常数
存在常数![]() ,使
,使![]() 对一切实数x均成立,
对一切实数x均成立,
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央国务院高度重视改善人民生活,始终把提高人民生活水平作为一切工作的出发点和落脚点城乡居民收入大幅增长,居民生活发生了翻天覆地的变化.下面是1949年及2015年~2018年中国居民人均可支配收入(元)统计图.以下结论中不正确的是( )
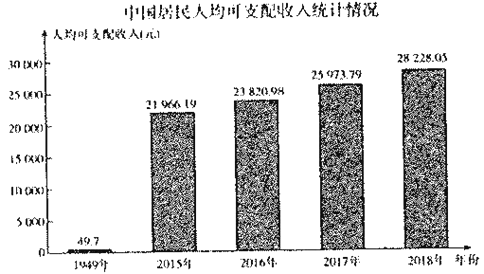
A.20l5年-2018年中国居民人均可支配收入与年份成正相关
B.2018年中居民人均可支配收入超过了1949年的500倍
C.2015年-2018年中国居民人均可支配收入平均超过了24000元
D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为发挥体育咋核心素养时代的独特育人价值,越来越多的中学生已将某些体育项目纳入到学生的必修课程,某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生抽取了100人进行调查.
班 级 | 一(1) | 一(2) | 一(3) | 一(4) | 一(5) | 一(6) | 一(7) | 一(8) | 一(9) | 一(10) |
市级比赛 获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
市级以上比 赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
(1)已知在被抽取的女生中有6名高一(1)班学生,其中3名对游泳有兴趣,现在从这6名学生中最忌抽取3人,求至少有2人对游泳有兴趣的概率;
(2)该研究性学习小组在调查发现,对游泳有兴趣的学生中有部分曾在市级以上游泳比赛中获奖,如上表所示,若从高一(8)班和高一(9)班获奖学生中随机各抽取2人进行跟踪调查.记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com