
����Ŀ����ͼ��ij�˳а���һ���������![]() ������ֲ��ݮ������
������ֲ��ݮ������![]() m��
m��![]() m.�ֹ滮������ͼ��ʾ�İ�Բ�������ϱ�Ĥ����
m.�ֹ滮������ͼ��ʾ�İ�Բ�������ϱ�Ĥ����![]() ����ÿ����Բ���ʹ��������Բ�ε�������涼���������ϱ�Ĥ����ͷ�����Բ��ƣ������ϱ�Ĥ�ļ۸�Ϊÿƽ����
����ÿ����Բ���ʹ��������Բ�ε�������涼���������ϱ�Ĥ����ͷ�����Բ��ƣ������ϱ�Ĥ�ļ۸�Ϊÿƽ����![]() Ԫ�����⣬������ÿ������֮������
Ԫ�����⣬������ÿ������֮������![]() m���Ŀյ����ڽ�����ˮ��������С·����ͼ��
m���Ŀյ����ڽ�����ˮ��������С·����ͼ��![]() m�����ⲿ�ֽ������Ϊÿƽ����
m�����ⲿ�ֽ������Ϊÿƽ����![]() Ԫ.
Ԫ.
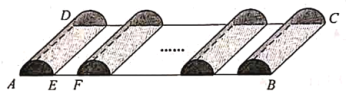
��1����![]() ʱ������һ�������������ϱ�Ĥ�����������С��������
ʱ������һ�������������ϱ�Ĥ�����������С��������![]() ��
��
��2����ȷ������ĸ�����ʹ������������õĺ���ͣ�����С�������![]() ȡ
ȡ![]() ��
��
���𰸡���1��![]() m2����2��
m2����2��![]() ��
��
��������
��1������ÿ����Բ���ʹ���ĵ���뾶Ϊ![]() ������
������![]() ʱ������
ʱ������![]() ���յأ��������Բ�뾶������������������
���յأ��������Բ�뾶������������������
��2����������õĺ�Ϊ![]() ���������⣬�õ�
���������⣬�õ�![]() �����ɻ�������ʽ������������.
�����ɻ�������ʽ������������.
�⣺��1����ÿ����Բ���ʹ���ĵ���뾶Ϊ![]() .
.
��![]() ʱ������
ʱ������![]() ���յأ�����
���յأ�����![]() m��
m��
����ÿ������ı���������������Ӵ����棩Ϊ
![]() (m2).
(m2).
����һ�������������ϱ�Ĥ�����Ϊ![]() m2.
m2.
��2����������õĺ�Ϊ![]() .
.
��Ϊ![]() ������ÿ������ı���������������Ӵ����棩Ϊ
������ÿ������ı���������������Ӵ����棩Ϊ
![]() ��
��
��![]()
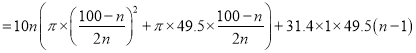
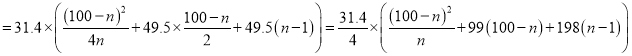
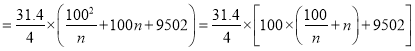
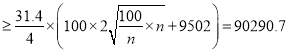 .
.
���ԣ����ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ȡ����Сֵ.
ȡ����Сֵ.
�𣺵�����ĸ���Ϊ![]() ��ʱ������������õĺ����.
��ʱ������������õĺ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��������ͬ�ļ�ֵ��
��������ͬ�ļ�ֵ��![]() ��
��![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���ڣ�1���������£���֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ![]() ��tΪ������������OΪ���㣬x���������Ϊ������ȡ��ͬ�ĵ�λ���Ƚ���������ϵ������C�ļ����귽��Ϊ
��tΪ������������OΪ���㣬x���������Ϊ������ȡ��ͬ�ĵ�λ���Ƚ���������ϵ������C�ļ����귽��Ϊ![]() .
.
��1��������C��ֱ�����귽�̼�ֱ��l����ͨ���̣�
��2������������C����ƽ��1����λ���ȣ��ٽ�����C�ϵ����е�ĺ������Ϊԭ����2�����õ�����![]() ��������
��������![]() �ϵĵ㵽ֱ��l�ľ�������ֵ.
�ϵĵ㵽ֱ��l�ľ�������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У���ABC�DZ߳�Ϊ6�ĵȱ������Σ�D��E�ֱ�ΪAA1��BC���е㣮
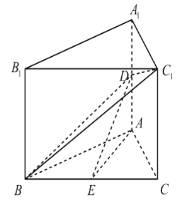
��1��֤����AE//ƽ��BDC1��
��2��������ֱ��BC1��AC���ɽǵ�����ֵΪ![]() ����DE��ƽ��BDC1���ɽǵ�����ֵ��
����DE��ƽ��BDC1���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�����˸��������ʵؾ��ȵ���������Ϸ���������£��������ĵ���֮��Ϊ4�ı���������ԭͶ���˼���Ͷ�����������ĵ���֮�Ͳ���4�ı��������ɶԷ�����Ͷ����
��1���涨��1�δ�С����ʼ��
��������ǰ4��Ͷ����С��ǡ��Ͷ��2�εĸ��ʣ�
����������Ϸ��ǰ4���У�С��Ͷ���Ĵ���Ϊ![]() �����������
�����������![]() �ķֲ�����������
�ķֲ�����������
��2������1�δ�С����ʼ�����![]() ����С��Ͷ���ĸ���
����С��Ͷ���ĸ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��ֱ��![]() �ھ���
�ھ���![]() ����Ӧ�ı任
����Ӧ�ı任![]() �µõ�ֱ��
�µõ�ֱ��![]() ����
����![]() �ķ���.
�ķ���.
��2����֪��![]() ������
������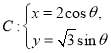 ��
��![]() ������
Ϊ������![]() ����һ�㣬
����һ�㣬![]() Ϊ����ԭ��ֱ��
Ϊ����ԭ��ֱ��![]() ����б��Ϊ
����б��Ϊ![]() �����
�����![]() ������.
������.
��3����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ž�������ҵ�������Ͼ�Ӫһ�Ҹɹ��꣬���۵ĸɹ��������ӡ����Ĺ������������ң��۸�����Ϊ120Ԫ/ǧ�ˡ�80Ԫ/ǧ�ˡ�70Ԫ/ǧ�ˡ�40Ԫǧ�ˣ�Ϊ�����������ž��������ָɹ����д���:һ�ι���ɹ����ܼ۴ﵽ150Ԫ���˿;��ٸ�x(2x��Z)Ԫ.ÿ�ʶ����˿�����֧���ɹ����ž���õ�֧�����80%.
�����˿�һ�ι������Ӻ�������1ǧ�ˣ���Ҫ֧��180Ԫ����x=________��
���ڴ�����У�Ϊ��֤�ž�ÿ�ʶ����õ��Ľ��������ڴ���ǰ�ܼ۵����ۣ���x�����ֵΪ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ����ĩ��ѧ�����У�Ϊͳ��ѧ���Ŀ����������ѧУ��2000��ѧ���������ȡ50��ѧ���Ŀ��Գɼ�������ѧ���ɼ�ȫ������65�ֵ�145��֮�䣨����150�֣�����ͳ�ƽ�������·�ʽ�ֳɰ��飺��һ��![]() ���ڶ���
���ڶ���![]() �������ڰ���
�������ڰ���![]() ����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣�
����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣�
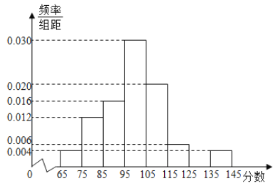
��1����������Ƶ�ʣ�
��2�����������ݹ��Ƹ�У��2000��ѧ����ο��Գɼ���ƽ���֣�ͬһ���е������ø���������е�ֵ������������ƽ��ֵ����
��3�����������ɼ����ڵ�����͵ڰ��������ѧ���������ȡ2���������ǵķֲ�ľ���ֵС��10�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪����![]() �ļ����귽����
�ļ����귽����![]() ���Լ���Ϊԭ�㣬����Ϊ
���Լ���Ϊԭ�㣬����Ϊ![]() ��������Ὠ��ƽ��ֱ������ϵ��ֱ��
��������Ὠ��ƽ��ֱ������ϵ��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ (
(![]() ������.
������.
(I)д��ֱ��![]() ��һ�㷽��������
��һ�㷽��������![]() ��ֱ�����귽�̣����ж����ǵ�λ�ù�ϵ��
��ֱ�����귽�̣����ж����ǵ�λ�ù�ϵ��
(II)������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ�����ƽ��
����λ���ȣ�����ƽ��![]() ����λ���ȣ��õ�����
����λ���ȣ��õ�����![]() ��������
��������![]() ���������任
���������任![]() �õ�����
�õ�����![]() ��������
��������![]() ����һ��Ϊ
����һ��Ϊ![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com