
【题目】(1)椭圆C:![]() +
+![]() =1(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
=1(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:![]()
![]() 为定值b2﹣a2.
为定值b2﹣a2.
(2)由(1)类比可得如下真命题:双曲线C:![]() =1(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则
=1(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则![]() 为定值.请写出这个定值(不要求给出解题过程).
为定值.请写出这个定值(不要求给出解题过程).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设点P(x0,y0),x0≠±a,依题意,得A(﹣a,0),B(a,0),从而得直线PA的方程,继而求得点M,N的纵坐标,得到yMyN=![]() ,把点P(x0,y0),代入椭圆方程可求得yMyN=
,把点P(x0,y0),代入椭圆方程可求得yMyN=![]() =b2,从而得
=b2,从而得![]() =b2﹣a2.
=b2﹣a2.
(2)类比(1)的结论,可得![]() 的值.
的值.
(1)证明:设点P(x0,y0),x0≠±a,
依题意,得A(﹣a,0),B(a,0),
∴直线PA的方程为y=![]() (x+a)
(x+a)
令x=0,得yM=![]()
同理得yN=![]()
∴yMyN=![]() ,
,
∵点P(x0,y0)是椭圆C上一点,
∴![]() =1,
=1,![]() =
=![]() (a2﹣
(a2﹣![]() ),
),
∴yMyN=![]() =b2,
=b2,
![]() =(a,yN),
=(a,yN),![]() =(﹣a,yM),
=(﹣a,yM),
∴![]() =﹣a2+yMyN=b2﹣a2
=﹣a2+yMyN=b2﹣a2
(2)﹣(a2+b2)


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 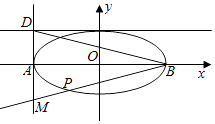
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)当a=2时,求函数f(x)的最值;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温/℃ | 18 | 13 | 10 | -1 |
用电量/度 | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程![]() 中,
中,![]() ≈-2,预测当气温为-4℃时,用电量为多少.
≈-2,预测当气温为-4℃时,用电量为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin2x+1﹣
sin2x+1﹣ ![]() .
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,若f(x)≥log2t恒成立,求t的取值范围.
]时,若f(x)≥log2t恒成立,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com