
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(Ⅱ)设![]() ,若函数
,若函数![]() 在定义域上为单调增函数,求
在定义域上为单调增函数,求![]() 的最大整数值.
的最大整数值.
科目:高中数学 来源: 题型:
【题目】如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, ![]() =
= ![]() =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
=2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
A.γ<α<β
B.α<γ<β
C.α<β<γ
D.β<γ<α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).
(细管长度忽略不计).
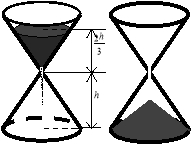
(1)如果该沙漏每秒钟漏下0.02cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?
(2)细沙全部漏入下部后,恰好堆成个一盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解交通运行压力,某市公交系统实施疏堵工程.现调取某路公交车早高峰时段全程运输时间(单位:分钟)的数据,从疏堵工程完成前的数据中随机抽取5个数据,记为![]() 组;从疏堵工程完成后的数据中随机抽取5个数据,记为
组;从疏堵工程完成后的数据中随机抽取5个数据,记为![]() 组.
组.
![]() 组:
组:![]()
![]()
![]()
![]()
![]()
![]() 组:
组:![]()
![]()
![]()
![]()
![]()
(Ⅰ)该路公交车全程运输时间不超过![]() 分钟,称为“正点运行”.从
分钟,称为“正点运行”.从![]() ,
,![]() 两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;
两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;
(Ⅱ)试比较![]() ,
,![]() 两组数据方差的大小(不要求计算),并说明其实际意义.
两组数据方差的大小(不要求计算),并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率e=
的离心率e=![]() , 原点到过A(a,0),B(0,﹣b)两点的直线的距离是
, 原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() .
.
(1)求椭圆的方程;
(2)已知直线y=kx+1(k≠0)交椭圆于不同的两点E,F,且E,F都在以B为圆心的圆上,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
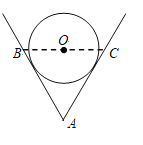
【题目】如图,一个底面水平放置的倒圆锥形容器,它的轴截面是正三角形,容器内有一定量的水,水深为![]() . 若在容器内放入一个半径为 1 的铁球后,水面所在的平面恰好经过铁球的球心
. 若在容器内放入一个半径为 1 的铁球后,水面所在的平面恰好经过铁球的球心![]() (水没有溢出),则
(水没有溢出),则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信公司从所在地的1000名使用4G手机用户中,随机抽取了20名,对其收集每日使用流量(单位:M)进行统计,得到如下数据:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢看书是否与性别有关,某校调查小组就“是否喜欢看书”这个问题,在全校随机调研了100名学生.
(1)完成下列![]() 列联表:
列联表:
喜欢看书 | 不喜欢看书 | 合计 | |
女生 | 15 | 50 | |
男生 | 25 | ||
合计 | 100 |
(2)能否在犯错率不超过0.025的前提下认为“喜欢看书与性别有关”.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com