
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
【答案】(1)![]() ;(2)直线AB过定点Q(0,﹣2).
;(2)直线AB过定点Q(0,﹣2).
【解析】试题分析:(1)根据椭圆的几何性质得到椭圆方程;(2)先由特殊情况得到结果,再考虑一般情况,联立直线和椭圆得到二次函数,根据韦达定理,和向量坐标化的方法,得到结果。
(Ⅰ)由椭圆的离心率e=![]() ,则a2=4b2, 将P(2,1)代入椭圆
,则a2=4b2, 将P(2,1)代入椭圆![]() ,则
,则![]() ,解得:b2=2,则a2=8, ∴椭圆的方程为:
,解得:b2=2,则a2=8, ∴椭圆的方程为: ![]() ;
;
(Ⅱ)当M,N分别是短轴的端点时,显然直线AB为y轴,所以若直线过定点,这个定点一点在y轴上,
当M,N不是短轴的端点时,设直线AB的方程为y=kx+t,设A(x1,y1)、B(x2,y2),
由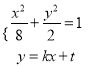 消去y得(1+4k2)x2+8ktx+4t2﹣8=0,·则△=16(8k2﹣t2+2)>0,
消去y得(1+4k2)x2+8ktx+4t2﹣8=0,·则△=16(8k2﹣t2+2)>0,
x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又直线PA的方程为y﹣1=![]() (x﹣2),即y﹣1=
(x﹣2),即y﹣1=![]() (x﹣2),
(x﹣2),
因此M点坐标为(0, ![]() ),同理可知:N(0,
),同理可知:N(0, ![]() ),
),
由![]() ,则
,则![]() +
+![]() =0,
=0,
化简整理得:(2﹣4k)x1x2﹣(2﹣4k+2t)(x1+x2)+8t=0,
则(2﹣4k)×![]() ﹣(2﹣4k+2t)(
﹣(2﹣4k+2t)(![]() )+8t=0,
)+8t=0,
当且仅当t=﹣2时,对任意的k都成立,直线AB过定点Q(0,﹣2).


科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:集合
满足:集合![]() 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数![]() 是等比源函数.
是等比源函数.
(![]() )判断下列函数:①
)判断下列函数:①![]() ;②
;②![]() ;③
;③![]() 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(![]() )判断函数
)判断函数![]() 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
(![]() )证明:
)证明: ![]() ,
, ![]() ,函数
,函数![]() 都是等比源函数.
都是等比源函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下,请根据此解答如下问题:
(1)求班级的总人数;
(2)将频率分布表及频率分布直方图的空余位置补充完整;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.
分组 | 频数 | 频率 |
[50,60) | 0.08 | |
[60,70) | 7 | |
[70,80) | 10 | |
[80,90) | ||
[90,100) | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的机坐标系中,直线
轴的非负半轴为极轴建立的机坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是双曲线 ![]() =1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
=1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双十一网购狂欢,快递业务量猛增.甲、乙两位快递员![]() 月
月![]() 日到
日到![]() 日每天送件数量的茎叶图如图所示.
日每天送件数量的茎叶图如图所示.
(Ⅰ)根据茎叶图判断哪个快递员的平均送件数量较多(写出结论即可);
(Ⅱ)求甲送件数量的平均数;
(Ⅲ)从乙送件数量中随机抽取![]() 个,求至少有一个送件数量超过甲的平均送件数量的概率.
个,求至少有一个送件数量超过甲的平均送件数量的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com