
【题目】已知函数![]() .
.
(Ⅰ)求函数y=f(x)图象的对称轴和对称中心;
(Ⅱ)若函数![]() ,
,![]() 的零点为x1,x2,求cos(x1﹣x2)的值.
的零点为x1,x2,求cos(x1﹣x2)的值.
【答案】(Ⅰ)对称轴方程为x![]() ,k∈Z,对称中心为(
,k∈Z,对称中心为(![]() ,0),k∈Z;(Ⅱ)±
,0),k∈Z;(Ⅱ)±![]() .
.
【解析】
(Ⅰ)先利用三角恒等变换化简目标函数,然后求解对称轴和对称中心;
(Ⅱ)先求出![]() 的零点,然后求解cos(x1﹣x2)的值.
的零点,然后求解cos(x1﹣x2)的值.
函数![]() sin4x
sin4x![]() cos4x=sin(4x
cos4x=sin(4x![]() ),
),
(Ⅰ)由4x![]() ,k∈Z,可得f(x)的对称轴方程为x
,k∈Z,可得f(x)的对称轴方程为x![]() ,k∈Z,
,k∈Z,
令4x![]() kπ,k∈Z,则x
kπ,k∈Z,则x![]() ,k∈Z,∴f(x)的对称中心为(
,k∈Z,∴f(x)的对称中心为(![]() ,0),k∈Z;
,0),k∈Z;
(Ⅱ)根据函数![]() ,可得g(x)=sin(4x
,可得g(x)=sin(4x![]() )
)![]() ,
,![]() 的零点为x1,x2,
的零点为x1,x2,
∴sin(4x1![]() )
)![]() 0,即sin(4x1
0,即sin(4x1![]() )
)![]() ,∴2sin(2x1
,∴2sin(2x1![]() )cos(2x1
)cos(2x1![]() )
)![]() ,
,
∴![]() ,∴
,∴![]() .
.
由(Ⅰ)知,f(x)在![]() 内的对称轴为x
内的对称轴为x![]() ,则x1+x2
,则x1+x2![]() ,∴x2
,∴x2![]() x1,
x1,
∴cos(x1﹣x2)=cos(x1﹣(![]() x1)=cos(2x1
x1)=cos(2x1![]() )=sin(
)=sin(![]() 2x1
2x1![]() )
)
=sin(2x1![]() )=sin(2x1
)=sin(2x1![]() )
)
![]()
=±![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,平面PAC垂直圆O所在平面,直线PC与圆O所在平面所成角为60°,PA⊥PC.
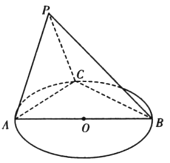
(1)证明:AP⊥平面PBC
(2)求二面角P—AB一C的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)求四边形![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,判断点
,判断点![]() 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
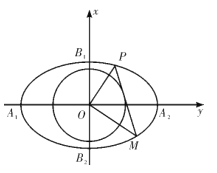
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种细菌的适宜生长温度为10℃~25℃,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:℃)变化的规律,收集数据如下:
(单位:℃)变化的规律,收集数据如下:
温度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖数量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
对数据进行初步处理后,得到了一些统计量的值,如下表所示:
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中![]() ,
,![]() .
.

(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表格数据,建立![]() 关于
关于![]() 的回归方程(结果精确到0.1);
的回归方程(结果精确到0.1);
(3)当温度为25℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二成估计分别为
的斜率和截距的最小二成估计分别为 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
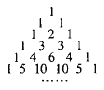
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,准线的方程为
,准线的方程为![]() ,
,![]() 为抛物线
为抛物线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的两条切线与
的两条切线与![]() 轴交于
轴交于![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若![]() ,求△
,求△![]() 面积
面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为x轴,其准线过点![]() .
.
(1)求抛物线C的方程;
(2)过抛物线焦点F作直线l,使得抛物线C上恰有三个点到直线l的距离都为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com