练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
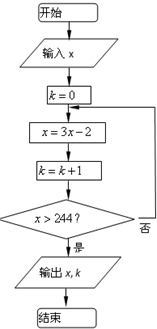
    按如图所示的程序框图运算，若输出k的值为2，则输入x的取值范围是
    84
    3
    ＜x≤82
    84
    3
    ＜x≤82
    ．
    分析：由框图知，此程序输出的k是循环次数，循环退出的条件是x＞244，由此关系得出不等式，求出x的取值范围即可．
    解答：解：依题意可知 
    244≥3x-2
    244＜3(3x-2)-2
    ，
    解得：
    84
    3
    ＜x≤82．
    故答案为：
    84
    3
    ＜x≤82．
    点评：本题考查循环结构，解题的关键是根据框图得出其运算律，从而得到x所满足的不等式，解不等式求出要求的范围，由运算规则得出不等式组是本题的难点，题后应好好体会此关系的转化．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    5、按如图所示的程序框图运算，若输入x=6，则输出k的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•莆田模拟）某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．
    （1）求n的值；
    （2）把在前排就坐的高二代表队6人分别记为a，b，c，d，e，f，现随机从中抽取2人上台抽奖．求a和b至少有一人上台抽奖的概率．
    （3）抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

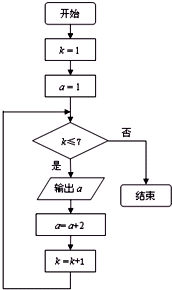    按如图所示的程序框图操作，若将输出的数按照输出的先后顺序排列，则得到数列{an}，则数列 {an}的通项公式是
    an=2n-1（n∈N+，n≤7）
    an=2n-1（n∈N+，n≤7）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    按如图所示的程序框图运算，若输入x=2，则输出k的值是
    5
    5
    ．

    查看答案和解析>>

    同步练习册答案