
分析 (1)令cn=an+1-an,通过cn+1-cn=1,说明{an+1-an}是以2为首项,1为公差的等差数列.
(2)由(1)知cn=n+1,求出an,化简$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$).利用裂项求和求解即可.
解答 解:(1)证明:令cn=an+1-an,
则cn+1-cn=(an+2-an+1)-(an+1-an)=an+2-2an+1+an=1(常数),
c1=a2-a1=2,
故{an+1-an}是以2为首项,1为公差的等差数列. …(4分)
(2)由(1)知cn=n+1,即an+1-an=n+1,
于是an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=
=n+(n-1)+…+2+1=$\frac{n(n+1)}{2}$,…(8分)
故$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$).
∴Sn=2(1-$\frac{1}{2}$)+2($\frac{1}{2}$-$\frac{1}{3}$)+2($\frac{1}{3}$-)+…+2($\frac{1}{n}$-$\frac{1}{n+1}$)
=2(1-$\frac{1}{n+1}$)
=$\frac{2n}{n+1}$. …(12分)
点评 本题考查数列求和,等差数列的判断,考查计算能力.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
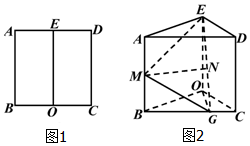 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com