
【题目】已知圆P过![]() .
.
(1)求圆P的方程;
(2)若过点![]() 的直线l被圆P所截得的弦长为8,求直线l的方程.
的直线l被圆P所截得的弦长为8,求直线l的方程.
科目:高中数学 来源: 题型:
【题目】某公司的甲、乙两名工程师因为工作需要,各自选购一台笔记本电脑.该公司提供了![]() 三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
型号 |
|
|
|
销量(台) | 2000 | 2000 | 4000 |
用户评分 | 8 | 6.5 | 9.5 |
若甲选购某款笔记本电脑的概率与对应的销量成正比,乙选购某款笔记本电脑的概率与对应的用户评分减去5的值成正比,且他们两人选购笔记本电脑互不影响.
(1)求甲、乙两人选购不同款笔记本电脑的概率;
(2)若公司给购买这三款笔记本电脑的员工一定的补贴,补贴标准如下表:
型号 |
|
|
|
补贴(千元) | 3 | 4 | 5 |
记甲、乙两人获得的公司补贴之和为![]() 千元,求
千元,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知抛物线C:y2=2px(p>0)的焦点为F,过F垂直于x轴的直线与C相交于A、B两点,△AOB的面积为2.
(1)求抛物线C的方程;
(2)若过P(![]() ,0)的直线与C相交于M,N两点,且
,0)的直线与C相交于M,N两点,且![]() 2
2![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】造纸术、印刷术、指南针、火药被称为中国古代四大发明,此说法最早由英国汉学家艾约瑟提出并为后来许多中国的历史学家所继承,普遍认为这四种发明对中国古代的政治,经济,文化的发展产生了巨大的推动作用.某小学三年级共有学生500名,随机抽查100名学生并提问中国古代四大发明,能说出两种发明的有45人,能说出3种及其以上发明的有32人,据此估计该校三级的500名学生中,对四大发明只能说出一种或一种也说不出的有( )
A.69人B.84人C.108人D.115人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.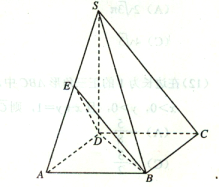
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com