练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆为圆上任一点.

    （1）求的最大值与最小值；

    （2）求的最大值与最小值.

    【答案】（1）最大值是，最小值是；（2）最大值是，最小值是.

    【解析】

    （2）试题分析：（1）是圆上的点与点连线的斜率，最大、最小值分别是过点的圆的两条切线的斜率.设切线的斜率为，利用圆心到直线的距离等于半径，求出斜率；（2）令，则，转化为线性规划问题求解，平移直线，当直线和圆有公共点时，的范围即可确定，且最值在直线与圆相切时取得.利用点到直线的距离公式，求得的取值范围.

    试题解析：

    （1）显然可以看作是点与点连线的斜率.令，如图所示，则其最大、最小值分别是过点的圆的两条切线的斜率.

    对上式整理得，

    ∴，

    ∴.

    故的最大值是，最小值是.

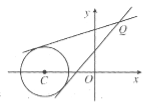
    （3）令，则可视为一组平行线，当直线和圆有公共点时，的范围即可确定，且最值在直线与圆相切时取得.

    依题意，得，取得，

    故的最大值是，最小值是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆,，过椭圆的右顶点和上顶点的直线与圆相切.

    （1）求椭圆的方程;

    （2）设是椭圆的上顶点, 过点分别作直线交椭圆于两点, 设这两条直线的斜率分别为,且,证明: 直线 过定点

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当x∈[1，4]时，求函数的值域；

    （2）如果对任意的x∈[1，4]，不等式恒成立，求实数k的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，其中a∈R.

    （Ⅰ)当a＝1时，判断f（x)的单调性；

    （Ⅱ)若g（x)在其定义域内为增函数，求正实数a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明对本班同学做调查，提出问题“你考试作弊吗？”这样的问法______（填“合理”或“不合理”），理由是______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）如图，点A，B是单位圆上的两点，A，B两点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，若点A的坐标为（，），记∠COA＝α．

    （Ⅰ）求的值；

    （Ⅱ）求cos∠COB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在上的函数的导函数为，且满足， ，当时有恒成立，若非负实数、满足， ，则的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】铁矿石A和B的含铁率为,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石

    的价格c如下表：

    b(万吨)

    （百万元）

    A

    50%

    1

    3

    B

    70%

    0．5

    6

    某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某企业的两座建筑物AB，CD的高度分别为20m和40m，其底部BD之间距离为20m．为响应创建文明城市号召，进行亮化改造，现欲在建筑物AB的顶部A处安装一投影设备，投影到建筑物CD上形成投影幕墙，既达到亮化目的又可以进行广告宣传．已知投影设备的投影张角∠EAF为，投影幕墙的高度EF越小，投影的图像越清晰．设投影光线的上边沿AE与水平线AG所成角为α，幕墙的高度EF为y（m）．

    （1）求y关于α的函数关系式，并求出定义域；

    （2）当投影的图像最清晰时，求幕墙EF的高度．

    查看答案和解析>>

    同步练习册答案