
分析 根据函数奇偶性的定义建立方程关系进行求解即可.
解答 解:∵f(x)=loga$\frac{1-mx}{x-1}$是奇函数,
∴f(-x)=-f(x),
即f(-x)+f(x)=0,
则loga$\frac{1+mx}{-x-1}$+loga$\frac{1-mx}{x-1}$=loga($\frac{1-mx}{x-1}$•$\frac{1+mx}{-x-1}$)=0,
则$\frac{1-mx}{x-1}$•$\frac{1+mx}{-x-1}$=$\frac{1-{m}^{2}{x}^{2}}{1-{x}^{2}}$=1,
即m2=1,则m=1或m=-1,
当m=1时,f(x)=loga$\frac{1-x}{x-1}$=loga(-1)无意义,
故m=-1,
故答案为:-1
点评 本题主要考查函数奇偶性的应用,根据奇偶性的定义建立方程是解决本题的关键.注意要进行检验.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
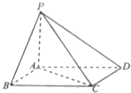 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=PA=1,且PA⊥平面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=PA=1,且PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 1007 | C. | 2016 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M+m=4 | B. | M+m=3 | C. | M-m=4 | D. | M-m=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 分组 | 频数 |
| 第一组 | [20,25) | 2 |
| 第二组 | [25,30) | a |
| 第三组 | [30,35) | b |
| 第四组 | [35,40) | c |
| 第五组 | [40,45) | d |
| 第六组 | [45,50] | e |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com