
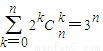 (n∈N);
(n∈N);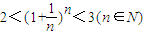 .
.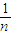 )n展开可得1+
)n展开可得1+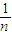 Cn1+
Cn1+ Cn2+…
Cn2+…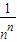 +Cnn=1+1++
+Cnn=1+1++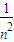 Cn2+…
Cn2+…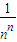 +Cnn;分析可得:(1+
+Cnn;分析可得:(1+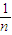 )n>2;另一方面,用放缩法分析,,(1+
)n>2;另一方面,用放缩法分析,,(1+ )n=1+1+
)n=1+1+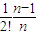 +
+ +…+
+…+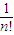 •
•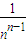 •(n-1)(n-2)…2•1<1+1+
•(n-1)(n-2)…2•1<1+1+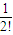 +
+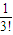 +…+
+…+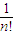 <1+1+
<1+1+ +
+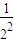 +…+
+…+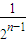 ;整理可得右式的证明,综合可证得原不等式.
;整理可得右式的证明,综合可证得原不等式.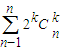 =左式;
=左式; )n=1+
)n=1+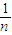 Cn1+
Cn1+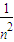 Cn2+…
Cn2+… +Cnn=1+1+
+Cnn=1+1+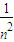 Cn2+…
Cn2+… +Cnn;①
+Cnn;①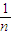 )n>2;
)n>2;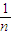 )n=1+1+
)n=1+1+ +
+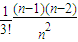 +…+
+…+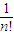 •
•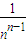 •(n-1)(n-2)…2•1
•(n-1)(n-2)…2•1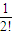 +
+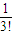 +…+
+…+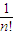 <1+1+
<1+1+ +
+ +…+
+…+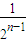
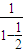 =3;
=3;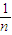 )n<3.
)n<3.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| A•4n+B |
| 2n |
| A•4n+B |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a1 |
| b1-1 |
| a2 |
| b2-1 |
| a3 |
| b3-1 |
| an |
| bn-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| yn |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 1-an |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com