Question

 [番茄花园1] 

已知数列{a_n}满足a₁＝0，a₂＝2，且对任意m、n∈N^*都有

a_2m－1＋a_2n－1＝2a_m＋n－1＋2(m－n)²

（Ⅰ）求a₃，a₅；

（Ⅱ）设b_n＝a_2n＋1－a_2n－1(n∈N^*)，证明：{b_n}是等差数列；

（Ⅲ）设c_n＝(a_n+1－a_n)q^n－1(q≠0，n∈N^*)，求数列{c_n}的前n项和S_n.

 

 

 

---

 [番茄花园1]1.

Answer 1

【答案】

 [番茄花园1] 

问题的能力.

解：(1)由题意，零m＝2,n－1,可得a₃＝2a₂－a₁＋2＝6

       再令m＝3,n＝1，可得a₅＝2a₃－a₁＋8＝20………………………………2分

(2)当n∈N ^*时，由已知(以n＋2代替m)可得

a_2n＋3＋a_2n－1＝2a_2n＋1＋8

于是[a_2(n＋1)＋1－a_2(n＋1)－1]－(a_2n＋1－a_2n－1)＝8  

即  b_n＋1－b_n＝8

所以{b_n}是公差为8的等差数列………………………………………………5分

(3)由(1)(2)解答可知{b_n}是首项为b₁＝a₃－a₁＝6,公差为8的等差数列

本小题主要考查数列的基础知识和化归、分类整合等数学思想，以及推理论证、分析与解决

则b_n＝8n－2，即a_2n+=1－a_2n－1＝8n－2

另由已知(令m＝1)可得

a_n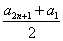＝-(n－1)².

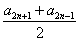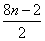那么a_n＋1－a_n＝－2n＋1  

           ＝－2n＋1

           ＝2n

于是c_n＝2nq^n－1.

当q＝1时，S_n＝2＋4＋6＋……＋2n＝n(n＋1)

当q≠1时，S_n＝2·q⁰＋4·q¹＋6·q²＋……＋2n·q^n－1.

两边同乘以q，可得

          qS_n＝2·q¹＋4·q²＋6·q³＋……＋2n·qⁿ.

上述两式相减得

       (1－q)S_n＝2(1＋q＋q²＋……＋q^n－1)－2nqⁿ  

               ＝2·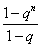－2nqⁿ

               ＝2·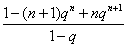

所以S_n＝2·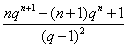

综上所述，S_n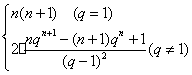＝…………………………12分

 

---

 [番茄花园1]21.