
【题目】如图,在矩形 ![]() 中,
中, ![]() 分别为
分别为 ![]() 的中点,现将
的中点,现将 ![]() 沿
沿 ![]() 折起,得四棱锥
折起,得四棱锥 ![]()
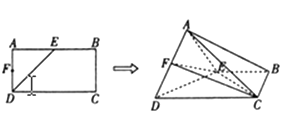
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)若平面 ![]() 平面
平面 ![]() ,求四面体
,求四面体 ![]() 的体积.
的体积.
【答案】
(1)证明:取线段 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,因为
,因为 ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() ,且
,且 ![]() ,在折叠前,四边形
,在折叠前,四边形 ![]() 为矩形,
为矩形, ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() ,且
,且 ![]() .
. ![]() ,且
,且 ![]() ,所以四边形
,所以四边形 ![]() 为平行四边形,故
为平行四边形,故 ![]() ,又
,又 ![]() 平面
平面 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
(2)解:在折叠前,四边形 ![]() 为矩形,
为矩形, ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() 都是等腰直角三角形,且
都是等腰直角三角形,且 ![]() ,所以
,所以 ![]() ,且
,且 ![]() .又
.又![]() ,又平面
,又平面 ![]() 平面
平面 ![]() ,平面
,平面 ![]() 平面
平面 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]() ,即
,即 ![]() 为三棱锥
为三棱锥 ![]() 的高.因为
的高.因为 ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() ,所以四面体
,所以四面体 ![]() 的体积
的体积 ![]() 。
。
【解析】(1)要证明线面平行,即证明面外的一条线与面内的一条线平行即可。
(2)先利用已知条件及面面垂直的性质,找出三棱锥C-EFD的高,再根据F是AD的中点这一性质求出底面面积,最后利用体积公式![]() 求出即可。
求出即可。
【考点精析】利用直线与平面平行的判定和直线与平面平行的性质对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-x2-2x,g(x)= 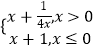
(1)求g[f(1)]的值;
(2)若方程g[f(x)]-a=0有4个实数根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)= ![]() ﹣
﹣ ![]() (x为实常数).
(x为实常数).
(1)当a=1时,求函数φ(x)=f(x)﹣g(x)在x∈[4,+∞)上的最小值;
(2)若方程e2f(x)=g(x)(其中e=2.71828…)在区间[ ![]() ]上有解,求实数a的取值范围.
]上有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x<2},B={x|3﹣2x>0},则( )
A.A∩B={x|x< ![]() }
}
B.A∩B=?
C.A∪B={x|x< ![]() }
}
D.AUB=R
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() :
: ![]() 的焦点为
的焦点为 ![]() ,过点
,过点 ![]() 分别作两条直线
分别作两条直线 ![]() ,
, ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 、
、 ![]() 两点,直线
两点,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 、
、 ![]() 两点,若
两点,若 ![]() 与
与 ![]() 的斜率的平方和为1,则
的斜率的平方和为1,则 ![]() 的最小值为( )
的最小值为( )
A.16
B.20
C.24
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20 , 接下来的两项是20 , 21 , 再接下来的三项是20 , 21 , 22 , 依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440
B.330
C.220
D.110
查看答案和解析>>
科目:高中数学 来源: 题型:
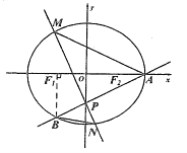
【题目】如图,椭圆 ![]() 的右顶点为
的右顶点为 ![]() ,左、右焦点分别为
,左、右焦点分别为 ![]() ,过点
,过点 ![]() 且斜率为
且斜率为 ![]() 的直线与
的直线与 ![]() 轴交于点
轴交于点 ![]() ,与椭圆交于另一个点
,与椭圆交于另一个点 ![]() ,且点
,且点 ![]() 在
在 ![]() 轴上的射影恰好为点
轴上的射影恰好为点 ![]() .
.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过点 ![]() 的直线与椭圆交于
的直线与椭圆交于 ![]() 两点(
两点( ![]() 不与
不与 ![]() 重合),若
重合),若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com