
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
【答案】A
【解析】
根据线面平行性质定理,结合线面垂直的定义,可得①是真命题;根据面面平行的性质结合线面垂直的性质,可得②是真命题;在正方体中举出反例,可得平行于同一个平面的两条直线不一定平行,垂直于同一个平面和两个平面也不一定平行,可得③④不正确.由此可得本题的答案.
解:对于①,因为![]() ,所以经过
,所以经过![]() 作平面
作平面![]() ,使
,使![]() ,可得
,可得![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() ,结合
,结合![]() 得
得![]() .由此可得①是真命题;
.由此可得①是真命题;
对于②,因为![]() 且
且![]() ,所以
,所以![]() ,结合
,结合![]() ,可得
,可得![]() ,故②是真命题;
,故②是真命题;
对于③,设直线![]() 、
、![]() 是位于正方体上底面所在平面内的相交直线,
是位于正方体上底面所在平面内的相交直线,
而平面![]() 是正方体下底面所在的平面,
是正方体下底面所在的平面,
则有![]() 且
且![]() 成立,但不能推出
成立,但不能推出![]() ,故③不正确;
,故③不正确;
对于④,设平面![]() 、
、![]() 、
、![]() 是位于正方体经过同一个顶点的三个面,
是位于正方体经过同一个顶点的三个面,
则有![]() 且
且![]() ,但是
,但是![]() ,推不出
,推不出![]() ,故④不正确.
,故④不正确.
综上所述,其中正确命题的序号是①和②
故选:![]()


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2sinx,-1),
=(2sinx,-1),![]() ,函数f(x)=
,函数f(x)=![]() .
.
(1)求函数f(x)的对称中心;
(2)设△ABC的内角A,B,C所对的边为a,b,c,且a2=bc,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1000名,各车间男、女工人数如下表:已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0.15.
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
(1)求x的值.
(2)现用分层抽样的方法在全厂抽取50名工人,则应在第三车间抽取多少名工人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,
,![]() (
(![]() 且
且![]() ).
).
(1)求![]() 的值;
的值;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 为等差数列?若存在,求出
为等差数列?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDNPM中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AB=AP=2,PM∥AB,PN∥AD,PM=PN=1.

(1)求证:MN⊥PC;
(2)求平面MNC与平面APMB所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=3an+1(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD底面
平面ABCD底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
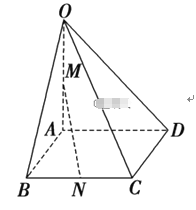
(1)求直线MN与直线CD所成角的余弦值;
(2)求直线OB与平面OCD所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com