
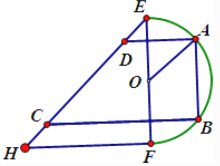
【题目】为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆![]() 及等腰直角三角形
及等腰直角三角形![]() ,其中
,其中![]() ,为裁剪出面积尽可能大的梯形铁片
,为裁剪出面积尽可能大的梯形铁片![]() (不计损耗),将点
(不计损耗),将点![]() 放在弧
放在弧![]() 上,点
上,点![]() 放在斜边
放在斜边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)求梯形铁片![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试确定![]() 的值,使得梯形铁片
的值,使得梯形铁片![]() 的面积
的面积![]() 最大,并求出最大值.
最大,并求出最大值.
科目:高中数学 来源: 题型:
【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是( ![]() ,
, ![]() ),则当0≤t≤12时,动点A的纵坐标y关于 t(单位:秒)的函数的单调递增区间是 .
),则当0≤t≤12时,动点A的纵坐标y关于 t(单位:秒)的函数的单调递增区间是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=2,AD=4,PA⊥底面ABCD,PD与底面ABCD成30°角,E是PD的中点. 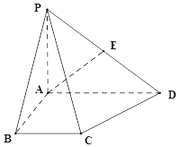
(1)点H在AC上且EH⊥AC,求 ![]() 的坐标;
的坐标;
(2)求AE与平面PCD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2![]() .
.
(1)求角A的大小;
(2)若D为BC的中点,求线段AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C的对边分别为a,b,c,且a,b,c成等比数列
(1)若sinC=2sinA,求cosB的值;
(2)求角B的最大值.并判断此时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲船以每小时15 ![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里,当甲船航行40分钟到达A2处时,乙船航行到甲船的南偏西45°方向的B2处,此时两船相距10海里,问乙船每小时航行多少海里?
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里,当甲船航行40分钟到达A2处时,乙船航行到甲船的南偏西45°方向的B2处,此时两船相距10海里,问乙船每小时航行多少海里? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和a件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出a件正品时检测结束,已知前两次检测都没有检测出次品的概率为![]() .
.
(1) 求实数a的值;
(2) 若每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
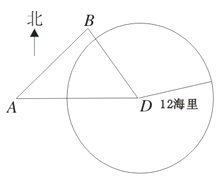
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处。
海里处。
(Ⅰ)求此时该外国船只与![]() 岛的距离;
岛的距离;
(Ⅱ)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.
(参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com