
【题目】设![]() 的内角
的内角![]() 所对的边分别是
所对的边分别是![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(Ⅰ)求角![]() ;
;
(Ⅱ)设![]() ,求
,求![]() 周长的最大值.
周长的最大值.
【答案】(1)60°;(2)6.
【解析】分析:(1)法一:由题意,利用正弦定理,化简得![]() ,即可求解角
,即可求解角![]() 的大小;
的大小;
法二:由题意,利用余弦定理化简得到![]() ,即
,即![]() ,即可求解角
,即可求解角![]() 的大小;
的大小;
(2)法一:由余弦定理及基本不等式,得![]() ,进而得
,进而得![]() 周长的最大值;法二:由正弦定理和三角恒等变换的公式化简整理得
周长的最大值;法二:由正弦定理和三角恒等变换的公式化简整理得![]() ,进而求解
,进而求解![]() 周长的最大值.
周长的最大值.
详解:(1)法一:由题,![]() ,
,
由正弦定理,![]() ,
,
即![]() ,解得
,解得![]() ,所以
,所以![]() .
.
法二:由题,由余弦定理得:![]()
![]() ,
,
解得![]() ,所以
,所以![]() .
.
(2)法一:由余弦定理及基本不等式,
![]()
![]() ,
,
得![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
故![]() 周长
周长![]() 的最大值为
的最大值为![]() .
.
法二:由正弦定理,![]() ,
,
故周长![]()
![]()
![]()
![]()
∵![]() ,∴当
,∴当![]() 时,周长
时,周长![]() 的最大值为
的最大值为![]() .
.
法三:如图,延长![]() 至
至![]() 使得
使得![]() ,则
,则![]() ,
,
于是,在![]() 中,由正弦定理:
中,由正弦定理:![]() ,
,
即![]() ,
,
故周长![]() ,
,
∵![]() ,∴当
,∴当![]() 时,周长
时,周长![]() 的最大值为
的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() ,过点
,过点 ![]() 的直线
的直线 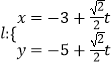 (
( ![]() 为参数)与曲线
为参数)与曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() 两点.
两点.
(1)求曲线 ![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线 ![]() 的普通方程;
的普通方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于命题的说法正确的有(填写所有正确命题的序号).
①“若 ![]() ,则函数
,则函数 ![]() (
( ![]() ,且
,且 ![]() )在其定义域内是减函数”是真命题;
)在其定义域内是减函数”是真命题;
②命题“若 ![]() ,则
,则 ![]() ”的否命题是“若
”的否命题是“若 ![]() ,则
,则 ![]() ”;
”;
③命题“若 ![]() ,
, ![]() 都是偶数,则
都是偶数,则 ![]() 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;
④命题“若 ![]() ,则
,则 ![]() ”与命题“若
”与命题“若 ![]() ,则
,则 ![]() ”等价.
”等价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com