
【题目】在中老年人群体中,肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系,调查了50位中老年人每周运动的总时长(单位:小时),将数据分成[0,4),[4,8),[8,14),[14,16),[16,20),[20,24]6组进行统计,并绘制出如图所示的柱形图.
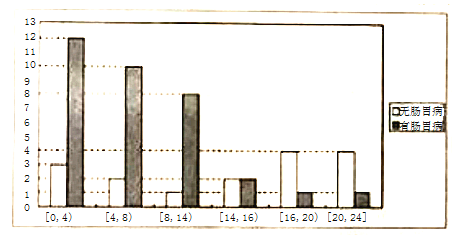
图中纵轴的数字表示对应区间的人数现规定:每周运动的总时长少于14小时为运动较少.
每周运动的总时长不少于14小时为运动较多.
(1)根据题意,完成下面的2×2列联表:
有肠胃病 | 无肠胃病 | 总计 | |
运动较多 | |||
运动较少 | |||
总计 |
(2)能否有99.9%的把握认为中老年人是否有肠胃病与运动有关?
附:K2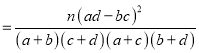 (n=a+b+c+d)
(n=a+b+c+d)
P(K2≥k) | 0.0.50 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】(1)若![]() ,是不等式
,是不等式![]() 成立的必要不充分条件,求实数的
成立的必要不充分条件,求实数的![]() 取值范围;
取值范围;
(2)已知集合![]() ,
,![]() .若“
.若“![]() ”是“
”是“![]() ”的充分条件,求实数
”的充分条件,求实数![]() 的取值范围;
的取值范围;
(3)已知命题“![]() ,
,![]() ”的否定为假命题,求实数
”的否定为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过
的准线经过![]() 的左焦点
的左焦点![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的上顶点且
的上顶点且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 地正西方向
地正西方向![]() 的
的![]() 处和正东方向
处和正东方向![]() 的
的![]() 处各一条正北方向的公路
处各一条正北方向的公路![]() 和
和![]() ,现计划在
,现计划在![]() 和
和![]() 路边各修建一个物流中心
路边各修建一个物流中心![]() 和
和![]() .
.
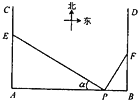
(1)若在![]() 处看
处看![]() ,
,![]() 的视角
的视角![]() ,在
,在![]() 处看
处看![]() 测得
测得![]() ,求
,求![]() ,
,![]() ;
;
(2)为缓解交通压力,决定修建两条互相垂直的公路![]() 和
和![]() ,设
,设![]() ,公路
,公路![]() 的每千米建设成本为
的每千米建设成本为![]() 万元,公路
万元,公路![]() 的每千米建设成本为
的每千米建设成本为![]() 万元.为节省建设成本,试确定
万元.为节省建设成本,试确定![]() ,
,![]() 的位置,使公路的总建设成本最小.
的位置,使公路的总建设成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 两焦点分别为
两焦点分别为![]() 、
、![]() ,且离心率
,且离心率![]() ;
;
(1)设E是直线![]() 与椭圆的一个交点,求
与椭圆的一个交点,求![]() 取最小值时椭圆的方程;
取最小值时椭圆的方程;
(2)已知![]() ,是否存在斜率为k的直线l与(1)中的椭圆交于不同的两点A、B,使得点N在线段AB的垂直平分线上,若存在,求出直线l在y轴上截距的范围;若不存在,说明理由。
,是否存在斜率为k的直线l与(1)中的椭圆交于不同的两点A、B,使得点N在线段AB的垂直平分线上,若存在,求出直线l在y轴上截距的范围;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,![]() ]上有两个实数解,求实数m的取值范围.
]上有两个实数解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com