
 ��֪��ԲCn��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n��a��b��1��n��N*����F1��F2����ԲC4�Ľ��㣬A��2��$\sqrt{2}$������ԲC4��һ�㣬��$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0��
��֪��ԲCn��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n��a��b��1��n��N*����F1��F2����ԲC4�Ľ��㣬A��2��$\sqrt{2}$������ԲC4��һ�㣬��$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0������ ��1����ԲC4�ķ���Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=4������$\frac{{x}^{2}}{4{a}^{2}}+\frac{{y}^{2}}{4{b}^{2}}$=1��������c2=a2-b2����F2��2c��0������$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0���ɵ�$\overrightarrow{A{F}_{2}}$��$\overrightarrow{{F}_{1}{F}_{2}}$��2c=2��$\frac{��2b��^{2}}{2a}$=$\frac{2{b}^{2}}{a}$=$\sqrt{2}$��2b4=a2=b2+1��������ɵó���
��2����i����ԲC2�ķ���Ϊ��$\frac{{x}^{2}}{2}$+y2=2 ����$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1����ԲC4�ķ���Ϊ��$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1����P��x0��y0������P����ԲC2�ϣ��ɵ�y02=$\frac{1}{2}$��4-x02����������б�ʼ��㹫ʽ����֤��k1k2Ϊ��ֵ��
��ii����ֱ��PF1�ķ���Ϊ��y=k1��x+2��ֱ��PF2�ķ���Ϊ��y=k2��x-2��������Բ����������Ԫ�����ã���2k12+1��x2+8k1x+8k12-8=0����E��x1��y1����F��x2��y2�������ø���ϵ���Ĺ�ϵ�ɵ�|EF|=$\sqrt{1+{k}_{1}^{2}}$$•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$��|MN|�����ã�i���Ľ��۴���|EF|?|MN|������֤����
��� �⣺��1���⣺��ԲC4�ķ���Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=4������$\frac{{x}^{2}}{4{a}^{2}}+\frac{{y}^{2}}{4{b}^{2}}$=1��
������c2=a2-b2 ��F2��2c��0����
��$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0����$\overrightarrow{A{F}_{2}}$��$\overrightarrow{{F}_{1}{F}_{2}}$��
����2c=2��$\frac{��2b��^{2}}{2a}$=$\frac{2{b}^{2}}{a}$=$\sqrt{2}$��2b4=a2=b2+1��
��2b4-b2-1=0��
��2b2+1����b2-1��=0��
��b2=1��a2=2��
����ԲCn�ķ���Ϊ��$\frac{x2}{2}$+y2=n��
��e2=$\frac{2{n}^{2}-{n}^{2}}{2{n}^{2}}$=$\frac{1}{2}$����e=$\frac{\sqrt{2}}{2}$��
��ԲC1�ķ���Ϊ��$\frac{x2}{2}$+y2=1��
��2����i��֤������ԲC2�ķ���Ϊ��$\frac{{x}^{2}}{2}$+y2=2 ����$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1��
��ԲC4�ķ���Ϊ��$\frac{{x}^{2}}{2}$+y2=4 ����$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1��
��F1��-2��0����F2��2��0������P��x0��y0����
��P����ԲC2�ϣ���$\frac{{x}_{0}^{2}}{4}+\frac{{y}_{0}^{2}}{2}$=1����y02=$\frac{1}{2}$��4-x02����
��k1k2=$\frac{{y}_{0}}{{x}_{0}+2}$•$\frac{{y}_{0}}{{x}_{0}-2}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$=$\frac{\frac{1}{2}��4-{x}_{0}^{2}��}{{x}_{0}^{2}-4}$=-$\frac{1}{2}$��
��ii����ֱ��PF1�ķ���Ϊ��y=k1��x+2��ֱ��PF2�ķ���Ϊ��y=k2��x-2����
���������飺$\left\{\begin{array}{l}{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\\{y={k}_{1}��x+2��}\end{array}\right.$ ��Ԫ�����ã���2k12+1��x2+8k1x+8k12-8=0����
��E��x1��y1����F��x2��y2������x1��x2�Ƿ��̢ٵ������⣬��Τ�ﶨ���ã�
x1+x2=-$\frac{8{k}_{1}}{2{k}_{1}^{2}+1}$��x1x2=$\frac{8{k}_{1}^{2}-8}{2{k}_{1}^{2}+1}$��
��|EF|=$\sqrt{1+{k}_{1}^{2}}$$•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{2}��1+{k}_{1}^{2}��}{2{k}_{1}^{2}+1}$��
ͬ����|MN|=$\frac{4\sqrt{2}��1+{k}_{2}^{2}��}{2{k}_{2}^{2}+1}$��
��|EF|?|MN|=$\frac{4\sqrt{2}��1+{k}_{1}^{2}��}{2{k}_{1}^{2}+1}$•$\frac{4\sqrt{2}��1+{k}_{2}^{2}��}{2{k}_{2}^{2}+1}$=32��$\frac{{k}_{1}^{2}{k}_{2}^{2}+{k}_{1}^{2}+{k}_{2}^{2}+1}{4{k}_{1}^{2}{k}_{2}^{2}+2{k}_{1}^{2}+2{k}_{2}^{2}+1}$=32��$\frac{��-\frac{1}{2}��^{2}+{k}_{1}^{2}+{k}_{2}^{2}+1}{4����-\frac{1}{2}��^{2}+2{k}_{1}^{2}+2{k}_{2}^{2}+1}$=$16+\frac{4}{{k}_{1}^{2}+{k}_{2}^{2}+1}$
=16+$\frac{4}{{k}_{1}^{2}+\frac{1}{4{k}_{1}^{2}}+1}$��18��
��|EF|?|MN|��0��
��|EF|?|MN|�ʣ�16��18]��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ�ҳ����⡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ����������ʽ�����ʣ���������������������������������⣮


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ƽ����һ�������㣬�������������������� | |
| B�� | ��������ֱ����ȷ��һ��ƽ�� | |
| C�� | ����A����ƽ����ڣ�����ƽ����ڣ��������ཻ��ֱ��b���ҵ�A��ֱ��b�� | |
| D�� | ����֪�ĸ��㲻���棬�������������㲻���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��6�� | B�� | ��-3��6$\sqrt{2}$�� | C�� | ��-6��6�� | D�� | ��-6��6$\sqrt{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R��x2+2��0 | B�� | ?x∉R��x2+2��0 | C�� | ?x��R��x2+2��0 | D�� | ?x��R��x2+2��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
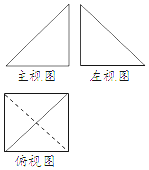 ��ͼ��ij�����������ͼ������ͼ��ȫ�ȵĵ���ֱ�������Σ�����ͼ�DZ߳�Ϊ2�������Σ���ô�������Ϊ��������
��ͼ��ij�����������ͼ������ͼ��ȫ�ȵĵ���ֱ�������Σ�����ͼ�DZ߳�Ϊ2�������Σ���ô�������Ϊ��������| A�� | $\frac{16}{3}$ | B�� | 4 | C�� | $\frac{8}{3}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com