解:(1)证法一:
(i)当n=1时,由已知a
1=1-2a
0,等式成立;
(ii)假设当n=k(k≥1)等式成立,
则
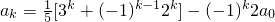
,
那么
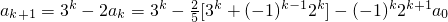
=
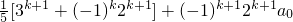
.
也就是说,当n=k+1时,等式也成立.
根据(i)和(ii),可知等式对任何n∈N,成立.
证法二:如果设a
n-a3
n=-2(a
n-1-a3
n-1),
用a
n=3
n-1-2a
n-1代入,可解出
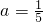
.
所以
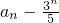
是公比为-2,
首项为
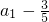
的等比数列.
∴
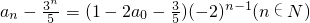
.
即
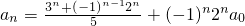
.
(2)解法一:由a
n通项公式
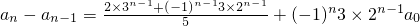
.
∴a
n>a
n-1(n∈N)等价于
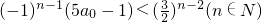
.①
(i)当n=2k-1,k=1,2,时,
①式即为
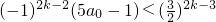
即为
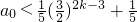
.
②式对k=1,2,都成立,
有
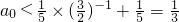
.
(ii)当n=2k,k=1,2时,
①式即为
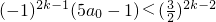
.
即为
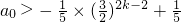
.
③式对k=1,2都成立,有
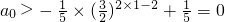
.
综上,①式对任意n∈N
*,成立,有
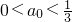
.
故a
0的取值范围为
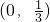
.
解法二:如果a
n>a
n-1(n∈N
*)成立,
特别取n=1,2有a
1-a
0=1-3a
0>0.a
2-a
1=6a
0>0.
因此
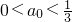
.下面证明当
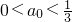
.时,
对任意n∈N
*,a
n-a
n-1>0.
由a
n的通项公式5(a
n-a
n-1)=2×3
n-1+(-1)
n-13×2
n-1+(-1)
n5×3×2
n-1a
0.
(i)当n=2k-1,k=1,2时,
5(a
n-a
n-1)=2×3
n-1+3×2
n-1-5×3×2
n-1a
0>2×2
n-1+3×2
n-1-5×3×2
n-1=0
(ii)当n=2k,k=1,2时,
5(a
n-a
n-1)=2×3
n-1-3×2
n-1+5×3×2
n-1a
0>2×3
n-1-3×2
n-1≥0.
故a
0的取值范围为
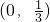
.
分析:(1)选择利用数学归纳法为妥,需要注意的是有归纳假设a
k到a
k+1的变形,利用归纳假设,注意目标的形式就能得到结果;另外可以利用递推数列来求得通项公式,当然需要对递推数列的a
n+1=pa
n+f(n)这种形式的处理要合适;这种形式的一般处理方法是:两边同时除以p
n+1或者是构造一个等比数列,构造法有一定的技巧,如本题可设a
n-a3
n=-2(a
n-1-a3
n-1),
(2)由(1)的结论可作差a
n-a
n-1>0并代入运算,由于含有(-1)
n的形式要注意对n=2k-1和n=2k进行讨论,只需取k=1,2时得到a
0的取值范围即可,另外一个思路是只需取n=1,2时得到a
0的范围,然后分n=2k-1和n=2k进行证明a
n-a
n-1>0.具体解法参见参考答案.
点评:本题主要考查数列、等比数列的概念,考查数学归纳法,考查灵活综合运用数学知识分析问题和解决问题的能力.对递推数列的a
n+1=pa
n+f(n)这种形式的考查是一个难点,同时除以p
n+1得到
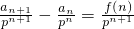
,然后用累加法得到
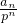
的等式可得结果,或者是构造一个等比数列a
n+1+kf(n)=p(a
n+kf(n))(不具有普适性).

 ;
;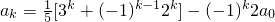 ,
,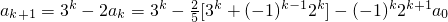
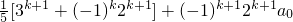 .
.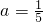 .
.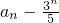 是公比为-2,
是公比为-2,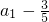 的等比数列.
的等比数列.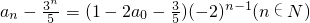 .
.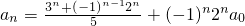 .
.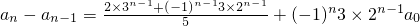 .
.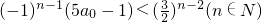 .①
.①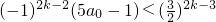
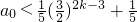 .
.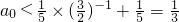 .
.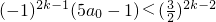 .
.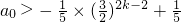 .
.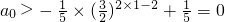 .
.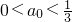 .
.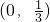 .
.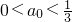 .下面证明当
.下面证明当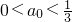 .时,
.时,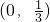 .
.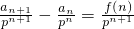 ,然后用累加法得到
,然后用累加法得到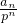 的等式可得结果,或者是构造一个等比数列an+1+kf(n)=p(an+kf(n))(不具有普适性).
的等式可得结果,或者是构造一个等比数列an+1+kf(n)=p(an+kf(n))(不具有普适性). 

 ;
; ;
; ;
;