Question

【题目】已知Sn为数列{an}的前n项和，且有a1=1，Sn+1=an+1（n∈N*）．
（1）求数列{an}的通项an；
（2）若bn= ，求数列{bn}的前n项和Tn；
（3）设ck= ，{ck}的前n项和为An ， 是否存在最小正整数m，使得不等式An＜m对任意正整数n恒成立？若存在，求出m的值；若不存在，说明理由．

Answer 1

【答案】
（1）解：当n=1时，a2=S1+1=a1+1=2；

当n≥2时，Sn+1=an+1，Sn﹣1+1=an，相减得an+1=2an，

又a2=2a1，

{an}是首项为1，公比为2的等比数列，

∴

（2）解：由（1）知 ，

∴ ，

∴ ，

，

两式相减得 = ，

∴

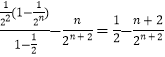（3）解：CK= =

= ．

∴ = = ．

若不等式∴ ＜m对任意正整数n恒成立，则m≥2，

∴存在最小正整数m=2，使不等式∴ ＜m对任意正整数n恒成立

【解析】（1）在数列递推式中取n=n﹣1得另一递推式，作差后即可证得数列为等比数列，代入等比数列的通项公式得答案；（2）把数列{an}的通项代入bn= ，然后利用错位相减法求数列{bn}的前n项和Tn；（3）把Sk ， Tk代入ck= ，整理后利用裂项相消法化简，放缩后可证得数列不等式．
【考点精析】掌握数列的前n项和是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系．