
【题目】设f(x)=asin2x+bcos2x(a,b∈R,ab≠0),若f(x)![]() 对一切x∈R恒成立,给出以下结论:
对一切x∈R恒成立,给出以下结论:
①![]() ;
;
②![]() ;
;
③f(x)的单调递增区间是![]() ;
;
④函数y=f(x)既不是奇函数也不是偶函数;
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交,其中正确结论为_____
【答案】①②④
【解析】
先转化f(x)=asin2x+bcos2x![]() ,根据f(x)
,根据f(x)![]() 对一切x∈R恒成立,得到
对一切x∈R恒成立,得到![]() 是f(x)的最大值或最小值,且f(x)的周期为
是f(x)的最大值或最小值,且f(x)的周期为![]() ,
,
①由![]() 相差四分之一个周期,由相邻最值点和零点间的关系判断.②利用轴对称判断,是否关于
相差四分之一个周期,由相邻最值点和零点间的关系判断.②利用轴对称判断,是否关于![]() 对称.③根据
对称.③根据![]() 是f(x)的最大值或最小值结合单调性判断.④由f(x)
是f(x)的最大值或最小值结合单调性判断.④由f(x)![]() 是奇函数,f(x)
是奇函数,f(x)![]() 是偶函数,判断.⑤根据三角函数的定义域和值域判断.
是偶函数,判断.⑤根据三角函数的定义域和值域判断.
设f(x)=asin2x+bcos2x![]() ,
,
因为f(x)![]() 对一切x∈R恒成立,
对一切x∈R恒成立,
所以![]() 是f(x)的最大值或最小值.
是f(x)的最大值或最小值.
又因为f(x)的周期为![]() ,
,
①![]() 为四分之一个周期,所以
为四分之一个周期,所以![]() ,故正确.
,故正确.
②因为![]() ,关于
,关于![]() 对称,所以
对称,所以![]() ,故正确.
,故正确.
③若![]() 是f(x)的最大值,则
是f(x)的最大值,则![]() ;f(x)的单调递减区间,故错误.
;f(x)的单调递减区间,故错误.
④由![]() ,所以函数不可能转化为f(x)
,所以函数不可能转化为f(x)![]() 或f(x)
或f(x)![]() 的形式,所以函数y=f(x)既不是奇函数也不是偶函数,故正确.
的形式,所以函数y=f(x)既不是奇函数也不是偶函数,故正确.
⑤若存在经过点(a,b)的直线与函数f(x)的图象不相交,则直线与横轴平行且![]() ,不成立,故错误.
,不成立,故错误.


科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
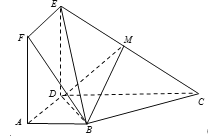
(Ⅰ) 若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅲ) 当平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,抛物线
,抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作两条斜率都存在的直线
作两条斜率都存在的直线![]() ,设
,设![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 是
是![]() 与
与![]() 的等比中项,求
的等比中项,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
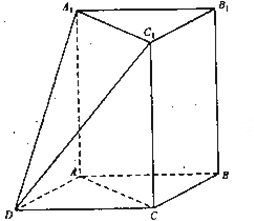
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com