
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以坐标原点
为极点,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为6,求实数
的最大距离为6,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,给出下列命题:
,给出下列命题:
①若数列![]() 既是等差数列,又是等比数列,则数列
既是等差数列,又是等比数列,则数列![]() 是常数列.
是常数列.
②若等差数列![]() 满足
满足![]() ,则数列
,则数列![]() 是常数列.
是常数列.
③若等比数列![]() 满足
满足![]() ,则数列
,则数列![]() 是常数列.
是常数列.
④若各项为正数的等比数列![]() 满足
满足![]() ,则数列
,则数列![]() 是常数列.
是常数列.
其中正确的命题个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率e=
的离心率e=![]() , 原点到过A(a,0),B(0,﹣b)两点的直线的距离是
, 原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() .
.
(1)求椭圆的方程;
(2)已知直线y=kx+1(k≠0)交椭圆于不同的两点E,F,且E,F都在以B为圆心的圆上,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() , …,
, …,![]() ,…有如下运算和结论:①
,…有如下运算和结论:①![]() ;②数列
;②数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列;③数列
,…是等比数列;③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .其中正确的结论是_____.(将你认为正确的结论序号都填上)
.其中正确的结论是_____.(将你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信公司从所在地的1000名使用4G手机用户中,随机抽取了20名,对其收集每日使用流量(单位:M)进行统计,得到如下数据:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设直线![]() 的方程为
的方程为![]() .若直线
.若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)过直线![]() :
:![]() 上的点
上的点![]() 作直线
作直线![]() ,若直线
,若直线![]() ,
,![]() 与
与![]() 轴围成的三角形的面积为2,则直线
轴围成的三角形的面积为2,则直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: 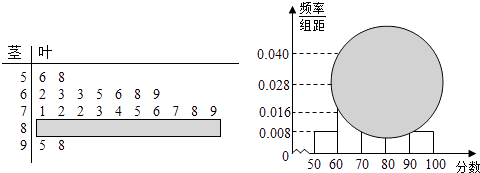
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:75(包含75分)分以上为良好,90分(包含90分)以上为优秀,要从分数在良好以上的试卷中任取两份分析学生失分情况,设在抽取的试卷中,分数为优秀的试卷份数为X,求X的概率分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com