
°æƒø°ø»ÁÕº£¨‘⁄’˝∑ΩÃÂ![]() ÷–£¨
÷–£¨ ![]() ∑÷± «¿‚
∑÷± «¿‚![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨ ![]() Œ™¿‚
Œ™¿‚![]() …œ“ªµ„£¨«““Ï√Ê÷±œþ
…œ“ªµ„£¨«““Ï√Ê÷±œþ![]() ”Î
”Î![]() À˘≥…Ω«µƒ”ýœ“÷µŒ™
À˘≥…Ω«µƒ”ýœ“÷µŒ™![]() .
.
£®1£©÷§√˜£∫ ![]() Œ™
Œ™![]() µƒ÷–µ„£ª
µƒ÷–µ„£ª
£®2£©«Û∆Ω√Ê![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…»Ò∂˛√ÊΩ«µƒ”ýœ“÷µ.
À˘≥…»Ò∂˛√ÊΩ«µƒ”ýœ“÷µ.
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£®2£©![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©“‘![]() Œ™◊¯±Í‘≠µ„£¨Ω®¡¢»ÁÕºÀ˘ 浃ø’º‰÷±Ω«◊¯±Íœµ
Œ™◊¯±Í‘≠µ„£¨Ω®¡¢»ÁÕºÀ˘ 浃ø’º‰÷±Ω«◊¯±Íœµ![]() £¨≤ª∑¡¡Ó’˝∑Ωõƒ¿‚≥§Œ™2£¨…Ë
£¨≤ª∑¡¡Ó’˝∑Ωõƒ¿‚≥§Œ™2£¨…Ë![]() £¨¿˚”√
£¨¿˚”√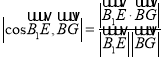 £¨Ω‚µ√
£¨Ω‚µ√![]() £¨º¥ø…÷§µ√£ª
£¨º¥ø…÷§µ√£ª
£®2£©∑÷±«Ûµ√∆Ω√Ê![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() µƒ∑®œÚ¡ø
µƒ∑®œÚ¡ø![]() £¨¿˚”√
£¨¿˚”√![]() «ÛΩ‚º¥ø….
«ÛΩ‚º¥ø….
‘Ã‚Ω‚Œˆ£∫
£®1£©÷§√˜£∫“‘![]() Œ™◊¯±Í‘≠µ„£¨Ω®¡¢»ÁÕºÀ˘ 浃ø’º‰÷±Ω«◊¯±Íœµ
Œ™◊¯±Í‘≠µ„£¨Ω®¡¢»ÁÕºÀ˘ 浃ø’º‰÷±Ω«◊¯±Íœµ![]() .
.
≤ª∑¡¡Ó’˝∑Ωõƒ¿‚≥§Œ™2£¨
‘Ú![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨
…Ë![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨ ![]() £¨
£¨
À˘“‘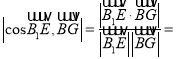
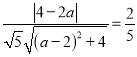 £¨
£¨
À˘“‘![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £®
£®![]() …·»•£©£¨º¥
…·»•£©£¨º¥![]() Œ™
Œ™![]() µƒ÷–µ„.
µƒ÷–µ„.
£®2£©Ω‚£∫”…£®1£©ø…µ√![]() £¨
£¨ ![]() £¨
£¨
…Ë![]() «∆Ω√Ê
«∆Ω√Ê![]() µƒ∑®œÚ¡ø£¨
µƒ∑®œÚ¡ø£¨
‘Ú![]() .¡Ó
.¡Ó![]() £¨µ√
£¨µ√![]() .
.
“◊µ√∆Ω√Ê![]() µƒ“ª∏ˆ∑®œÚ¡øŒ™
µƒ“ª∏ˆ∑®œÚ¡øŒ™![]() £¨
£¨
À˘“‘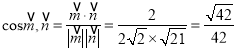 .
.
À˘“‘À˘«Û»Ò∂˛√ÊΩ«µƒ”ýœ“÷µŒ™![]() .
.
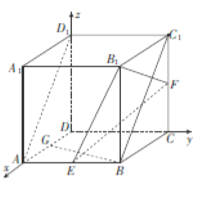
µ„涣∫ø’º‰œÚ¡øΩ‚¥¡¢Ãº∏∫ŒŒ µƒ“ª∞„≤Ω÷Ë «£∫£®1£©π€≤ÏÕº–Œ£¨Ω®¡¢«°µ±µƒø’º‰÷±Ω«◊¯±Íœµ£ª£®2£©–¥≥ˆœý”¶µ„µƒ◊¯±Í£¨«Û≥ˆœý”¶÷±œþµƒ∑ΩœÚœÚ¡ø£ª£®3£©…Ë≥ˆœý”¶∆Ω√ʵƒ∑®œÚ¡ø£¨¿˚”√¡Ω÷±œþ¥π÷± ˝¡øª˝Œ™¡„¡–≥ˆ∑Ω≥Ã◊È«Û≥ˆ∑®œÚ¡ø£ª£®4£©Ω´ø’º‰Œª÷√πÿœµ◊™ªØŒ™œÚ¡øπÿœµ£ª£®5£©∏˘æð∂®¿ÌΩ·¬€«Û≥ˆœý”¶µƒΩ«∫Õæý¿Î.
°æ–հøΩ‚¥Ã‚
°æΩ· ¯°ø
22
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ∂Ã÷·≥§Œ™2£¨«“Õ÷‘≤
µƒ∂Ã÷·≥§Œ™2£¨«“Õ÷‘≤![]() π˝µ„
π˝µ„ .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ë÷±œþ![]() π˝∂®µ„
π˝∂®µ„![]() £¨«“–±¬ Œ™
£¨«“–±¬ Œ™![]() £¨»ÙÕ÷‘≤
£¨»ÙÕ÷‘≤![]() …œ¥Ê‘⁄
…œ¥Ê‘⁄![]() ¡Ωµ„πÿ”⁄÷±œþ
¡Ωµ„πÿ”⁄÷±œþ![]() ∂‘≥∆£¨
∂‘≥∆£¨ ![]() Œ™◊¯±Í‘≠µ„£¨«Û
Œ™◊¯±Í‘≠µ„£¨«Û![]() µƒ»°÷µ∑∂Œßº∞
µƒ»°÷µ∑∂Œßº∞![]() √ʪ˝µƒ◊Ó¥Û÷µ.
√ʪ˝µƒ◊Ó¥Û÷µ.
°æ¥∞∏°ø£®1£©![]() £®2£©
£®2£©![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©Õ÷‘≤![]() µƒ∂Ã÷·≥§Œ™
µƒ∂Ã÷·≥§Œ™![]() £¨µ√
£¨µ√![]() £¨‘Ÿ”…Õ÷‘≤…œ“ªµ„¡–∑Ω≥ëÛΩ‚
£¨‘Ÿ”…Õ÷‘≤…œ“ªµ„¡–∑Ω≥ëÛΩ‚![]() º¥ø…£ª
º¥ø…£ª
£®2£©…Ë÷±œþ![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() £¨”ÎÕ÷‘≤¡™¡¢µ√
£¨”ÎÕ÷‘≤¡™¡¢µ√![]() £¨¿˚”√Œ§¥Ô∂®¿Ì«Ûµ√œþ∂Œ
£¨¿˚”√Œ§¥Ô∂®¿Ì«Ûµ√œþ∂Œ![]() µƒ÷–µ„Œ™
µƒ÷–µ„Œ™![]() £¨¥˙»Î÷±œþ
£¨¥˙»Î÷±œþ![]() ø…µ√£¨
ø…µ√£¨ ![]() £¨Ω·∫œ
£¨Ω·∫œ![]() º¥ø…«Ûµ√
º¥ø…«Ûµ√![]() µƒ»°÷µ∑∂Œß£¨‘Ÿ«Û
µƒ»°÷µ∑∂Œß£¨‘Ÿ«Û![]() ∫Õ‘≠µ„
∫Õ‘≠µ„![]() µΩ÷±œþ
µΩ÷±œþ![]() µƒæý¿Î
µƒæý¿Î![]() £¨Õ®π˝
£¨Õ®π˝![]() £¨¿˚”√Œ§¥Ô∂®¿Ì¥˙»Î«Û◊Ó÷µº¥ø….
£¨¿˚”√Œ§¥Ô∂®¿Ì¥˙»Î«Û◊Ó÷µº¥ø….
‘Ã‚Ω‚Œˆ£∫
£®1£©°þÕ÷‘≤![]() µƒ∂Ã÷·≥§Œ™2£¨°ý
µƒ∂Ã÷·≥§Œ™2£¨°ý![]() £¨º¥
£¨º¥![]() .
.
”÷µ„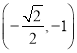 ‘⁄
‘⁄![]() …œ£¨°ý
…œ£¨°ý![]() £¨°ý
£¨°ý![]() .
.
°ýÕ÷‘≤![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() .
.
£®2£©”…“‚…Ë÷±œþ![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() £¨
£¨
”…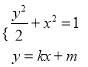 £¨œ˚»•
£¨œ˚»•![]() µ√£¨
µ√£¨ ![]() £¨
£¨
°ý![]() £¨º¥
£¨º¥![]() £¨¢Ÿ
£¨¢Ÿ
«“![]() £¨
£¨ ![]() £¨
£¨
°ýœþ∂Œ![]() ÷–µ„µƒ∫·◊¯±Í
÷–µ„µƒ∫·◊¯±Í![]() £¨◊ð◊¯±Í
£¨◊ð◊¯±Í![]() £¨
£¨
º¥œþ∂Œ![]() µƒ÷–µ„Œ™
µƒ÷–µ„Œ™![]() .
.
Ω´![]() ¥˙»Î÷±œþ
¥˙»Î÷±œþ![]() ø…µ√£¨
ø…µ√£¨ ![]() £¨¢⁄
£¨¢⁄
”…¢Ÿ£¨¢⁄ø…µ√£¨ ![]() £¨°ý
£¨°ý .
.
”÷![]()
 £¨
£¨
«“‘≠µ„![]() µΩ÷±œþ
µΩ÷±œþ![]() µƒæý¿Î
µƒæý¿Î £¨
£¨
°ý![]()
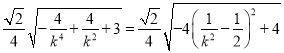 £¨
£¨
°þ![]() £¨°ý
£¨°ý![]() £¨°ýµ±
£¨°ýµ±![]() ±£¨
±£¨ ![]() »°µ√◊Ó¥Û÷µ
»°µ√◊Ó¥Û÷µ![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() £¨∫Ø ˝
£¨∫Ø ˝![]()
£®1£©Ã÷¬€![]() µƒµ•µ˜«¯º‰∫Õº´÷µ£ª
µƒµ•µ˜«¯º‰∫Õº´÷µ£ª
£®2£©Ω´∫Ø ˝![]() µƒÕºœÛœÚœ¬∆Ω“∆1∏ˆµ•Œª∫Ûµ√µΩ
µƒÕºœÛœÚœ¬∆Ω“∆1∏ˆµ•Œª∫Ûµ√µΩ![]() µƒÕºœÛ£¨«“
µƒÕºœÛ£¨«“![]() Œ™◊‘»ª∂‘ ˝µƒµ◊ ˝£©∫Õ
Œ™◊‘»ª∂‘ ˝µƒµ◊ ˝£©∫Õ![]() «∫Ø ˝
«∫Ø ˝![]() µƒ¡Ω∏ˆ≤ªÕ¨µƒ¡„µ„£¨«Û
µƒ¡Ω∏ˆ≤ªÕ¨µƒ¡„µ„£¨«Û![]() µƒ÷µ≤¢÷§√˜£∫
µƒ÷µ≤¢÷§√˜£∫ ![]() °£
°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ µ ˝a£æ0£¨b£æ0£¨∫Ø ˝f£®x£©=|x©Åa|©Å|x+b|µƒ◊Ó¥Û÷µŒ™3£Æ
£®I£© «Ûa+bµƒ÷µ£ª
£®¢Ú£©…Ë∫Ø ˝g£®x£©=©Åx2©Åax©Åb£¨»Ù∂‘”⁄x°ðaæ˘”–g£®x£©£ºf£®x£©£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂®“‘⁄[©Å ![]() £¨
£¨ ![]() ]µƒ∫Ø ˝f£®x£©=sinx£®cosx+1£©©Åax£¨»Ùy=f£®x£©Ωˆ”–“ª∏ˆ¡„µ„£¨‘Ú µ ˝aµƒ»°÷µ∑∂Œß «£® £©
]µƒ∫Ø ˝f£®x£©=sinx£®cosx+1£©©Åax£¨»Ùy=f£®x£©Ωˆ”–“ª∏ˆ¡„µ„£¨‘Ú µ ˝aµƒ»°÷µ∑∂Œß «£® £©
A.£® ![]() £¨2]
£¨2]
B.£®©Å°Þ£¨ ![]() £©°»[2£¨+°Þ£©
£©°»[2£¨+°Þ£©
C.[©Å ![]() £¨
£¨ ![]() £©
£©
D.£®©Å°Þ£¨©Å ![]() ]°»£®
]°»£® ![]() £¨+°Þ£©
£¨+°Þ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘ƒ≥–£∏þ“ªƒÍº∂—ß…˙≤Œº”…Á«¯∑˛ŒÒ¥Œ ˝Ω¯––Õ≥º∆£¨Àʪ˙≥È»°![]() √˚—ß…˙◊˜Œ™—˘±æ£¨µ√µΩ’‚
√˚—ß…˙◊˜Œ™—˘±æ£¨µ√µΩ’‚![]() √˚—ß…˙≤Œº”…Á«¯∑˛ŒÒµƒ¥Œ ˝.∏˘æð¥À ˝æð◊˜≥ˆ¡À∆µ ˝”Î∆µ¬ µƒÕ≥º∆±Ì∫Õ∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬£∫
√˚—ß…˙≤Œº”…Á«¯∑˛ŒÒµƒ¥Œ ˝.∏˘æð¥À ˝æð◊˜≥ˆ¡À∆µ ˝”Î∆µ¬ µƒÕ≥º∆±Ì∫Õ∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬£∫
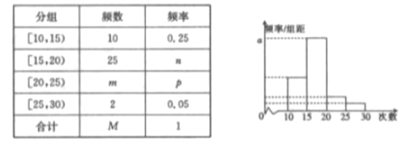
£®1£©«Û≥ˆ±Ì÷–![]() º∞Õº÷–
º∞Õº÷–![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©»Ù∏√–£∏þ“ª—ß…˙”–800»À£¨ ‘π¿º∆∏√–£∏þ“ª—ß…˙≤Œº”…Á«¯∑˛ŒÒµƒ¥Œ ˝‘⁄«¯º‰![]() ƒ⁄µƒ»À ˝.
ƒ⁄µƒ»À ˝.
°æ¥∞∏°ø£®1£©![]() £¨
£¨ ![]() £¨
£¨ ![]() £ª£®2£©
£ª£®2£©![]() »À.
»À.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©”…“‚£¨ ![]() ƒ⁄µƒ∆µ ˝ «10£¨∆µ¬ «0.25÷™£¨
ƒ⁄µƒ∆µ ˝ «10£¨∆µ¬ «0.25÷™£¨ ![]() £¨À˘“‘
£¨À˘“‘![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨ ![]() .£®2£©∏þ“ª—ß…˙”–800»À£¨∑÷◊È
.£®2£©∏þ“ª—ß…˙”–800»À£¨∑÷◊È![]() ƒ⁄µƒ∆µ¬ «
ƒ⁄µƒ∆µ¬ «![]() £¨»À ˝Œ™
£¨»À ˝Œ™![]() »À.
»À.
‘Ã‚Ω‚Œˆ£∫
£®1£©”…![]() ƒ⁄µƒ∆µ ˝ «10£¨∆µ¬ «0.25÷™£¨
ƒ⁄µƒ∆µ ˝ «10£¨∆µ¬ «0.25÷™£¨ ![]() £¨À˘“‘
£¨À˘“‘![]() .
.
“ÚŒ™∆µ ˝÷Æ∫ÕŒ™40£¨À˘“‘![]() £¨
£¨ ![]() .
.
![]() .
.
“ÚŒ™![]() «∂‘”¶∑÷◊È
«∂‘”¶∑÷◊È![]() µƒ∆µ¬ ”Î◊Èæýµƒ…ã¨À˘“‘
µƒ∆µ¬ ”Î◊Èæýµƒ…ã¨À˘“‘![]() .
.
£®2£©“ÚŒ™∏√–£∏þ“ª—ß…˙”–800»À£¨∑÷◊È![]() ƒ⁄µƒ∆µ¬ «
ƒ⁄µƒ∆µ¬ «![]() £¨
£¨
À˘“‘π¿º∆∏√–£∏þ“ª—ß…˙≤Œº”…Á«¯∑˛ŒÒµƒ¥Œ ˝‘⁄¥À«¯º‰ƒ⁄µƒ»À ˝Œ™![]() »À.
»À.
°æ–հøΩ‚¥Ã‚
°æΩ· ¯°ø
18
°æƒø°ø“—÷™÷±œþ![]() æ≠π˝≈◊ŒÔœþ
æ≠π˝≈◊ŒÔœþ![]() µƒΩπµ„
µƒΩπµ„![]() £¨«“”Î
£¨«“”Î![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„.
¡Ωµ„.
£®1£©…Ë![]() Œ™
Œ™![]() …œ“ª∂ص„£¨
…œ“ª∂ص„£¨ ![]() µΩ÷±œþ
µΩ÷±œþ![]() µƒæý¿ÎŒ™
µƒæý¿ÎŒ™![]() £¨µ„
£¨µ„![]() £¨«Û
£¨«Û![]() µƒ◊Ó–°÷µ£ª
µƒ◊Ó–°÷µ£ª
£®2£©«Û![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™‘≤Nµƒ±Í◊º∑Ω≥ÃŒ™(x£≠5)2£´(y£≠6)2£Ωa2(a>0).
(1)»Ùµ„M(6,9)‘⁄‘≤…œ£¨«Ûaµƒ÷µ£ª
(2)“—÷™µ„P(3,3)∫Õµ„Q(5,3)£¨œþ∂ŒPQ(≤ª∫¨∂Àµ„)”Α≤N”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨
£¨ ![]() £¨
£¨ ![]() £®∆‰÷–
£®∆‰÷–![]() «◊‘»ª∂‘ ˝µƒµ◊ ˝£©£Æ
«◊‘»ª∂‘ ˝µƒµ◊ ˝£©£Æ
£®1£©»Ù«˙œþ![]() ‘⁄µ„
‘⁄µ„![]() ¥¶µƒ«–œþ”Î÷±œþ
¥¶µƒ«–œþ”Î÷±œþ![]() ¥π÷±£¨«Û µ ˝
¥π÷±£¨«Û µ ˝![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©º«∫Ø ˝![]() £¨∆‰÷–
£¨∆‰÷–![]() £¨»Ù∫Ø ˝
£¨»Ù∫Ø ˝![]() ‘⁄
‘⁄![]() ƒ⁄¥Ê‘⁄¡Ω∏ˆº´÷µµ„£¨«Û µ ˝
ƒ⁄¥Ê‘⁄¡Ω∏ˆº´÷µµ„£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®3£©»Ù∂‘»Œ“‚![]() £¨
£¨ ![]() £¨«“
£¨«“![]() £¨æ˘”–
£¨æ˘”–![]() ≥…¡¢£¨«Û µ ˝
≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∏˜œÓæ˘Œ™’˝ ˝µƒ ˝¡–{an}µƒ«∞nœÓ∫ÕSn£æ1£¨«“6Sn=£®an+1£©£®an+2£©£¨n° N* £Æ
£®1£©«Û{an}µƒÕ®œÓπ´ Ω£ª
£®2£©»Ù ˝¡–{bn}¬˙◊„bn= ![]() £¨«Û{bn}µƒ«∞nœÓ∫Õ£Æ
£¨«Û{bn}µƒ«∞nœÓ∫Õ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂®“‘⁄R…œµƒ∫Ø ˝![]() ¬˙◊„
¬˙◊„![]() ,µ±
,µ±![]() ±◊Д–
±◊Д–![]()
![]() £¨»Ù
£¨»Ù![]() ,‘Ú µ ˝
,‘Ú µ ˝![]() µƒ»°÷µ∑∂Œß «_________.
µƒ»°÷µ∑∂Œß «_________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com