
【题目】如图,已知正四棱锥P﹣ABCD中,PA=AB=2,点M,N分别在PA,BD上,且 ![]() =
= ![]() .
. 
(1)求异面直线MN与PC所成角的大小;
(2)求二面角N﹣PC﹣B的余弦值.
【答案】
(1)解:设AC与BD的交点为O,AB=PA=2.以点O为坐标原点,
![]() ,
, ![]() ,
, ![]() 方向分别是x轴、y轴、z轴正方向,建立空间直角坐标系O﹣xyz.
方向分别是x轴、y轴、z轴正方向,建立空间直角坐标系O﹣xyz.

则A(1,﹣1,0),B(1,1,0),C(﹣1,1,0),D(﹣1,﹣1,0),…(2分)
设P(0,0,p),则 ![]() =(﹣1,1,p),又AP=2,
=(﹣1,1,p),又AP=2,
∴1+1+p2=4,∴p= ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() =(
=( ![]() ),
),
![]() =(
=( ![]() ),
),
∴ ![]() =(﹣1,1,﹣
=(﹣1,1,﹣ ![]() ),
), ![]() =(0,
=(0, ![]() ,﹣
,﹣ ![]() ),
),
设异面直线MN与PC所成角为θ,
则cosθ=  =
= ![]() =
= ![]() .
.
θ=30°,
∴异面直线MN与PC所成角为30°
(2)解: ![]() =(﹣1,1,﹣
=(﹣1,1,﹣ ![]() ),
), ![]() =(1,1,﹣
=(1,1,﹣ ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,﹣
,﹣ ![]() ),
),
设平面PBC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 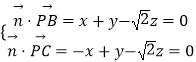 ,取z=1,得
,取z=1,得 ![]() =(0,
=(0, ![]() ,1),
,1),
设平面PNC的法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,取c=1,得
,取c=1,得 ![]() =(
=( ![]() ,2
,2 ![]() ,1),
,1),
设二面角N﹣PC﹣B的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角N﹣PC﹣B的余弦值为 ![]() .
.
【解析】(1)设AC与BD的交点为O,AB=PA=2.以点O为坐标原点, ![]() ,
, ![]() ,
, ![]() 方向分别是x轴、y轴、z轴正方向,建立空间直角坐标系O﹣xyz.利用向量法能求出异面直线MN与PC所成角.(2)求出平面PBC的法向量和平面PNC的法向量,利用向量法能求出二面角N﹣PC﹣B的余弦值.
方向分别是x轴、y轴、z轴正方向,建立空间直角坐标系O﹣xyz.利用向量法能求出异面直线MN与PC所成角.(2)求出平面PBC的法向量和平面PNC的法向量,利用向量法能求出二面角N﹣PC﹣B的余弦值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+cx(a>0),其图象在点(1,f(1))处的切线与直线 x﹣6y+21=0垂直,导函数
f′(x)的最小值为﹣12.
(1)求函数f(x)的解析式;
(2)求y=f(x)在x∈[﹣2,2]的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() =l (a>b>0)的焦距为2,离心率为
=l (a>b>0)的焦距为2,离心率为 ![]() ,椭圆的右顶点为A.
,椭圆的右顶点为A.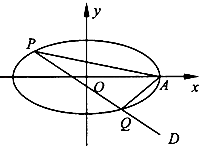
(1)求该椭圆的方程:
(2)过点D( ![]() ,﹣
,﹣ ![]() )作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量 ![]() =[
=[ ![]() ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如下程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( ) 
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 底面
底面![]() ,
, ![]() ,过点
,过点![]() 的平面与棱
的平面与棱![]() ,
, ![]() ,
, ![]() 分别交于点
分别交于点![]() ,
, ![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() 三点均不在棱的端点处).
三点均不在棱的端点处).

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(Ⅲ)直线![]() 是否可能与平面
是否可能与平面![]() 平行?证明你的结论.
平行?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为 ![]() ,各局比赛的结果都相互独立,第1局甲当裁判.
,各局比赛的结果都相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com