
分析 (1)当$a=-\frac{1}{3}时$,函数$f(x)=-\frac{2}{3}x+\frac{1}{3x}+lnx$,x>0,利用导数法,可得函数的单调区间
(2)若f(x)在(0,+∞)上是单调函数,则$f′(x)=2a+\frac{a}{{x}^{2}}+\frac{1}{x}$=$\frac{2{ax}^{2}+x+a}{{x}^{2}}$≥0,或$f′(x)=2a+\frac{a}{{x}^{2}}+\frac{1}{x}$=$\frac{2{ax}^{2}+x+a}{{x}^{2}}$≤0恒成立,分类讨论,可得a的取值范围.
解答 解:(1)当$a=-\frac{1}{3}时$,函数$f(x)=-\frac{2}{3}x+\frac{1}{3x}+lnx$,x>0,
则$f′(x)=-\frac{2}{3}-\frac{1}{3{x}^{2}}+\frac{1}{x}$=$-\frac{2{x}^{2}-3x+1}{3{x}^{2}}$,
令f′(x)=0,则x=$\frac{1}{2}$,或x=1,
当x∈(0,$\frac{1}{2}$)∪(1,+∞)时,f′(x)<0;当x∈($\frac{1}{2}$,1)时,f′(x)>0,
故函数$f(x)=-\frac{2}{3}x+\frac{1}{3x}+lnx$的单调递减区间为:(0,$\frac{1}{2}$)和(1,+∞);
单调递增区间为:($\frac{1}{2}$,1);
(2)若f(x)在(0,+∞)上是单调函数,
则$f′(x)=2a+\frac{a}{{x}^{2}}+\frac{1}{x}$=$\frac{2{ax}^{2}+x+a}{{x}^{2}}$≥0,或$f′(x)=2a+\frac{a}{{x}^{2}}+\frac{1}{x}$=$\frac{2{ax}^{2}+x+a}{{x}^{2}}$≤0恒成立,
当a=0时,f′(x)>0恒成立,满足条件;
当a>0时,f′(x)>0恒成立,满足条件;
当a<0时,则$\frac{8{a}^{2}-1}{8a}≤0$,解得:a≤-$\frac{\sqrt{2}}{4}$,
综上所述,a≤-$\frac{\sqrt{2}}{4}$,或a≥0
点评 本题考查的知识点函数的单调性,导数符号与原函数单调性的关系,恒成立问题,分类讨论思想,难度中档.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| A. | 0.35 | B. | 0.45 | C. | 0.55 | D. | 0.65 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x+1}$ | B. | y=2x-1 | C. | y=-|x| | D. | y=x2-3x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
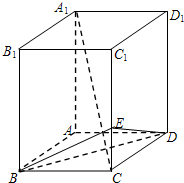 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com