
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
分析 实数a,b,c满足a2+2b2+3c2=1,kd 0≤a2+2b2≤1,令a=rcosθ,b=$\frac{\sqrt{2}}{2}rsinθ$,θ∈[0,2π),0≤r≤1.h代入化简即可得出.
解答 解:实数a,b,c满足a2+2b2+3c2=1,∴0≤a2+2b2≤1,
令a=rcosθ,b=$\frac{\sqrt{2}}{2}rsinθ$,θ∈[0,2π),0≤r≤1.
则a+2b=rcosθ+$\sqrt{2}$rsinθ=$\sqrt{3}r(\frac{1}{\sqrt{3}}cosθ+\frac{\sqrt{2}}{\sqrt{3}}sinθ)$=$\sqrt{3}r$sin(θ+φ)≤$\sqrt{3}$,
∴其最大值是$\sqrt{3}$,
故选:A.
点评 本题考查了通过三角函数换元求最值、不等式的性质,考查了推理能力与计算能力,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
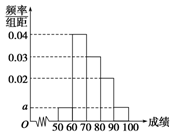 某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | $10\sqrt{3}$ | C. | 15 | D. | $15\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
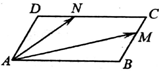 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )| A. | [0,3] | B. | [1,4] | C. | [2,5] | D. | [1,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com