
【题目】在平面直角坐标系xOy中,椭圆![]() 的左、右顶点分别为A、B,右焦点为F,且点F满足
的左、右顶点分别为A、B,右焦点为F,且点F满足![]() ,由椭圆C的四个顶点围成的四边形面积为
,由椭圆C的四个顶点围成的四边形面积为![]() .过点
.过点![]() 的直线TA,TB与此椭圆分别交于点
的直线TA,TB与此椭圆分别交于点![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
(1)求椭圆C的标准方程;
(2)当T在直线![]() 时,直线MN是否过x轴上的一定点?若是,求出该定点的坐标;若不是,请说明理由.
时,直线MN是否过x轴上的一定点?若是,求出该定点的坐标;若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一个最高点为(![]() ),与之相邻的一个对称中心为
),与之相邻的一个对称中心为![]() ,将f(x)的图象向右平移
,将f(x)的图象向右平移![]() 个单位长度得到函数g(x)的图象,则( )
个单位长度得到函数g(x)的图象,则( )
A.g(x)为偶函数
B.g(x)的一个单调递增区间为![]()
C.g(x)为奇函数
D.函数g(x)在![]() 上有两个零点
上有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线C:
中,抛物线C:![]() (
(![]() )的焦点为
)的焦点为![]()
(1)动直线l过F点且与抛物线C交于M,N两点,点M在y轴的左侧,过点M作抛物线C准线的垂线,垂足为M1,点E在![]() 上,且满足
上,且满足![]()
![]() 连接
连接![]() 并延长交y轴于点D,
并延长交y轴于点D,![]() 的面积为
的面积为![]() ,求抛物线C的方程及D点的纵坐标;
,求抛物线C的方程及D点的纵坐标;
(2)点H为抛物线C准线上任一点,过H作抛物线C的两条切线![]() ,
,![]() ,切点为A,B,证明直线
,切点为A,B,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
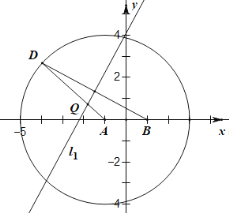
【题目】如图,已知圆![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,点
内一个定点,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() .当点
.当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为椭圆
的轨迹为椭圆![]() .
.
(1)![]() 分别为椭圆
分别为椭圆![]() 的左右焦点,
的左右焦点,![]() 为椭圆上任意一点,若
为椭圆上任意一点,若![]() ,求
,求![]() 的面积;
的面积;
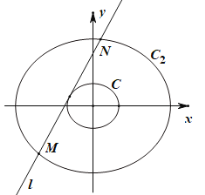
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() (
(![]() ,且
,且![]() ),则称椭圆
),则称椭圆![]() 是椭圆
是椭圆![]() 的
的![]() 倍相似椭圆.已知
倍相似椭圆.已知![]() 是椭圆
是椭圆![]() 的
的![]() 倍相似椭圆,若椭圆
倍相似椭圆,若椭圆![]() 的任意一条切线
的任意一条切线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() 、
、![]() ,试求弦长
,试求弦长![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设![]() ,用
,用![]() 表示不超过
表示不超过![]() 的最大整数,则
的最大整数,则![]() 称为高斯函数,例如:
称为高斯函数,例如:![]() ,
,![]() .已知函数
.已知函数![]() ,函数
,函数![]() ,则下列命题中真命题的个数是( )
,则下列命题中真命题的个数是( )
①![]() 图象关于
图象关于![]() 对称;
对称;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上是增函数;
上是增函数;
④![]() 的值域是
的值域是![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为生产一种精密管件研发了一台生产该精密管件的车床,该精密管件有内外两个口径,监管部门规定“口径误差”的计算方式为:管件内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() 则“口径误差”为
则“口径误差”为![]() 只要“口径误差”不超过
只要“口径误差”不超过![]() 就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
(Ⅰ)以上述样本的频率作为概率,在昼夜两个批次中分别抽取2件产品,求其中恰有1件不合格产品的概率;
(Ⅱ)若每批次各生产1000件,已知每件产品的成本为5元,每件合格品的利润为10元;若对产品检验,则每件产品的检验费用为2.5元;若有不合格品进入用户手中,则工厂要对用户赔偿,这时生产的每件不合格品工厂要损失25元.以上述样本的频率作为概率,以总利润的期望值为决策依据,分析是否要对每个批次的所有产品作检测?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.
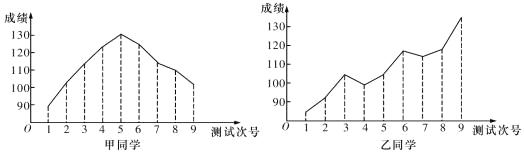
①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间![]() 内;
内;
③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关;
④乙同学连续九次测验成绩每一次均有明显进步.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C所对边的边长,且C=![]() ,a+b=λc(其中λ>1).
,a+b=λc(其中λ>1).
(1)若λ=![]() 时,证明:△ABC为直角三角形;
时,证明:△ABC为直角三角形;
(2)若![]() ·
·![]() =
=![]() λ2,且c=3,求λ的值.
λ2,且c=3,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com