
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为矩形, 且侧面
为矩形, 且侧面![]() 平面
平面![]() ,侧面
,侧面![]() 平面
平面![]() ,
,![]() 为正三角形,
为正三角形,![]()

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
![]() 因为
因为![]() ,所以
,所以![]() 平面
平面![]() ,由线面平行的性质定理推出结果
,由线面平行的性质定理推出结果
![]() 解法一:过
解法一:过![]() 作
作![]() 交
交![]() 于
于![]() ,结合
,结合![]() 可得
可得![]() 平面
平面![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,所以
,所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角,然后解三角形;
所成角,然后解三角形;
解法二:以![]() 的中点为原点,建立空间坐标系
的中点为原点,建立空间坐标系![]() ,设
,设![]() ,设
,设![]() 与面
与面![]() 所成的角为
所成的角为![]() ,计算平面
,计算平面![]() 的一个法向量为
的一个法向量为![]() ,计算平面
,计算平面![]() 的一个法向量为
的一个法向量为![]() ,解得
,解得![]() ,代入求出结果
,代入求出结果
(1)因为![]() ,所以
,所以![]() 平面
平面![]() ;
;
又因为![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,由线面平行的性质定理知
,由线面平行的性质定理知![]() .
.
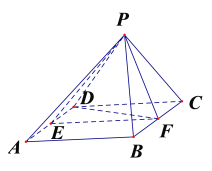
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,所以
,所以![]() .因为侧面
.因为侧面![]() 平面
平面![]() ,侧面
,侧面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,所以
,所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角.
所成角.
又因为![]() ,所以
,所以![]() ,于是在
,于是在![]() 中,
中,![]() .
.
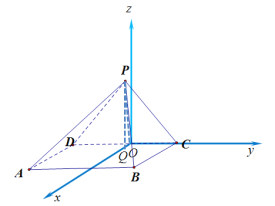
解法二:以![]() 的中点为原点,建立空间坐标系
的中点为原点,建立空间坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,设
,设![]() 与面
与面![]() 所成的角为
所成的角为![]() ,由题意
,由题意![]() 点在面
点在面![]() 的射影
的射影![]() 必在
必在![]() 轴上,且由
轴上,且由![]() 是边长为2的正三角形得
是边长为2的正三角形得![]() ,所以
,所以
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
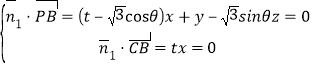 ,解得
,解得![]() ,
,
因为![]()
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
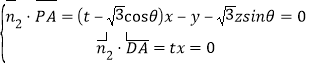 ,解得
,解得![]() ,
,
![]() ,
,
所以![]() ,
,![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,于是
,于是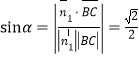 .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥B-AEDC中,平面AEDC⊥平面ABC,F为BC的中点,P为BD的中点,且AE//DC,∠ACD=∠BAC=90°,DC=AC=AB=2AE
(1)证明:EP⊥平面BCD;
(2)若DC=2,求三棱锥E-BDF的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
车流量(x万辆) | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
空气质量指数y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
(1)根据表中周一到周五的数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
附:回归方程![]() 中斜率和截距最小二乘估计公式分别为:
中斜率和截距最小二乘估计公式分别为:
 其中:
其中:![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为常数,函数
为常数,函数![]() ,给出以下结论:
,给出以下结论:
(1)若![]() ,则
,则![]() 存在唯一零点
存在唯一零点
(2)若![]() ,则
,则![]()
(3)若![]() 有两个极值点
有两个极值点![]() ,则
,则![]()
其中正确结论的个数是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某建筑工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料,某调查小组抄录了该工程施工地某月前![]() 天的降水量的数据,绘制得到降水量的折线图,如下图所示.
天的降水量的数据,绘制得到降水量的折线图,如下图所示.

(1)根据降水量的折线图,分别求该工程施工延误天数![]() 的频率;
的频率;
(2)以(1)中的频率作为概率,求工期延误天数![]() 的分布列及数学期望与方差.
的分布列及数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-![]() .
.
(1)求证:f(x)是R上的单调减函数.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com