
如图甲,在平面四边形ABCD中,已知
 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
(1)证明:见解析;(2)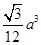 .
.
解析试题分析:(1)注意分析折叠前后变化的关系及不变化的关系.在图甲中可得 ;
;
在图乙中,可得AB⊥CD.根据DC⊥BC,即可得到DC⊥平面ABC.
(2)首先根据E,F分别为AC,AD的中点,得到EF//CD,根据(1)知,DC⊥平面ABC,得到EF⊥平面ABC,从而得到
在图甲中,根据给定角度及长度,计算“不变量”,得,BD=2 ,BC=
,BC=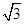
 ,EF=
,EF= CD=
CD=
 ,
,
利用体积公式计算即得所求.
解答本题的关键是确定“垂直关系”,这也是难点所在,平时学习中,应特别注意转化意识的培养,等体积转化的方法,是立体几何中常用方法之一.
(1)证明:在图甲中∵ 且
且 ∴
∴ ,
,
即 1分
1分
在图乙中,∵平面ABD⊥平面BDC , 且平面ABD∩平面BDC=BD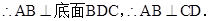 4分
4分
又 ,
,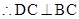 ,且
,且 ,∴DC⊥平面ABC. 6分
,∴DC⊥平面ABC. 6分
(2)解: , 7分
, 7分
又由(1)知,DC⊥平面ABC,∴EF⊥平面ABC, 8分
所以, 9分
9分
在图甲中, 
由 得,
得, ,
, 10分
10分 ,
, 11分
11分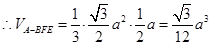 12分
12分
考点:平行关系,垂直关系,几何体的体积.


科目:高中数学 来源: 题型:解答题
如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC=3,侧面PBC⊥底面ABCD,O是BC的中点.
(1)求证:DC∥平面PAB;
(2)求四棱锥P﹣ABCD的体积.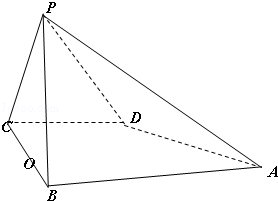
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=600,E为PA的中点,F为PC上不同于P、C的任意一点.
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1﹣A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(1)证明:中截面DEFG是梯形;
(2)在△ABC中,记BC=a,BC边上的高为h,面积为S.在估测三角形ABC区域内正下方的矿藏储量(即多面体A1B1C1﹣A2B2C2的体积V)时,可用近似公式V估=S中﹣h来估算.已知V= (d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.
(d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.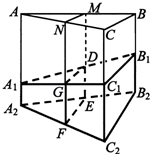
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知矩形 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
(1)求圆柱体的侧面积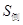 的值;
的值;
(2)若 是半圆弧
是半圆弧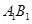 的中点,点
的中点,点 在半径
在半径 上,且
上,且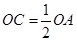 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在边长为a的正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com