
【题目】“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2019年春节期间,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.2元,2.9元,3.3元,5.9元,4.8元,商家从这5名顾客中随机抽取3人赠送饮水杯.

(1)求获得饮水杯的三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数x与商家每天的净利润y元,得到7组数据,如表所示,并作出了散点图.

(i)直接根据散点图判断,![]() 与
与![]() 出哪一个适合作为每天的净利润的回归方程类型.
出哪一个适合作为每天的净利润的回归方程类型.
(ii)根据(i)的判断,建立y关于x的回归方程;若商家当天的净利润至少是1400元,估计使用支付宝付款的人数至少是多少?(a,b,c,d的值取整数)
参考数据:
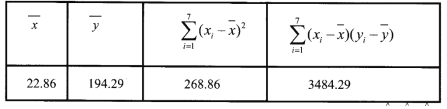
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为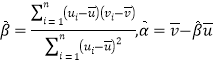 .
.
【答案】(1)![]() ;(2)(ⅰ)y=a+bx,(ⅱ)
;(2)(ⅰ)y=a+bx,(ⅱ)![]() ,至少是116人
,至少是116人
【解析】
(1)记“获得水杯的三人中至少有一人的红包超过5元”为事件M,5名顾客中红包超过5元的两人分别记为A1,A2,不足5元的三人分别记为B1,B2,B3,利用古典概型概率公式求解即可;(2)(i)根据散点图判断,y=a+bx适合;(ii)求出回归直线方程,推出结果即可.
(1)记“获得水杯的三人中至少有一人的红包超过5元”为事件M,5名顾客中红包超过5元的两人分别记为A1,A2,不足5元的三人分别记为B1,B2,B3,从这5名顾客中随机抽取3人,抽取情况如下:A1A2B1,A1A2B2,A1A2B3,A1B1B2,A1B1B3,A1B2B3,A2B1B2,A2B1B3,A2B2B3,B1B2B3,共10种,其中至少有一人的红包超过5元的是前9种情况,
所以![]() .
.
(2)(ⅰ)根据散点图可判断,选择y=a+bx作为每天的净利润的回归方程类型比较适合.
(ⅱ)由最小二乘法求得系数,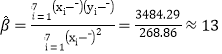
所以![]() ,
,
所以y关于x的回归方程为![]() =﹣103+13x.
=﹣103+13x.
若商家当天的净利润至少是1400元,则1400=-103+13x,解得![]()
故使用支付宝付款的人数至少是116人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电子计算机诞生于20世纪中叶,是人类最伟大的技术发明之一.计算机利用二进制存储信息,其中最基本单位是“位(bit)”,1位只能存放2种不同的信息:0或l,分别通过电路的断或通实现.“字节(Byte)”是更大的存储单位,1Byte=8bit,因此1字节可存放从00000000(2)至11111111(2)共256种不同的信息.将这256个二进制数中,所有恰有相邻两位数是1其余各位数均是0的所有数相加,则计算结果用十进制表示为
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完n片金片总共需要的次数为an,可推得a1=1,an+1=2an+1.如图是求移动次数在1000次以上的最小片数的程序框图模型,则输出的结果是( )
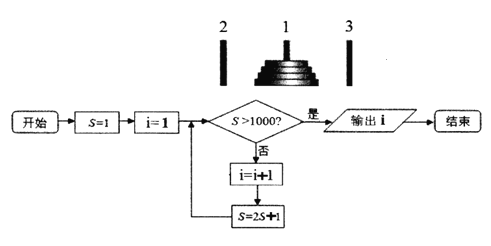
A. 8B. 9C. 10D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
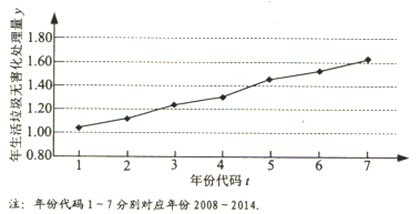
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的底面边长和侧棱长都为2,
的底面边长和侧棱长都为2,![]() 是
是![]() 的中点.
的中点.
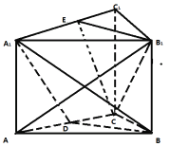
(1)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在指出点
,若存在指出点![]() 在线段
在线段![]() 上的位置,若不存在,请说明理由;
上的位置,若不存在,请说明理由;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3-2x2+3x(x∈R)的图象为曲线C.
x3-2x2+3x(x∈R)的图象为曲线C.
(1)求过曲线C上任意一点切线斜率的取值范围;
(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C的切点的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com