
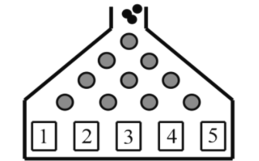
【题目】如图,高尔顿板是英国生物统计学家高尔顿设计的用来研究随机现象的模型,它是在一块竖起的木板上钉上一排排互相平行,水平间隔相等的圆柱形铁钉,并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央,从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两钉的间隙,又碰到下一排铁钉,如此继续下去,在最底层的5个出口处各放置一个容器接住小球,那么,小球落入1号容器的概率是______,若取4个小球进行试验,设其中落入4号容器的小球个数为x,则x的数学期望是______.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为![]() ,乙每次投球命中的概率为
,乙每次投球命中的概率为![]() ,且各次投球互不影响.
,且各次投球互不影响.
(1)经过1轮投球,记甲的得分为![]() ,求
,求![]() 的分布列;
的分布列;
(2)若经过![]() 轮投球,用
轮投球,用![]() 表示经过第
表示经过第![]() 轮投球,累计得分,甲的得分高于乙的得分的概率.
轮投球,累计得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机计算可估计得
,经过计算机计算可估计得![]() ,请根据①中
,请根据①中![]() 的值分别写出a,c关于b的表达式,并由此求出数列
的值分别写出a,c关于b的表达式,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击“新冠肺炎”,全国各地“停课不停学”,各学校都开展了在线课堂,组织学生在线学习,并自主安排时间完成相应作业为了解学生的学习效率,某在线教育平台统计了部分高三备考学生每天完成数学作业所需的平均时间,绘制了如图所示的频率分布直方图.
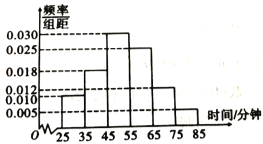
(1)如果学生在完成在线课程后每天平均自主学习时间(完成各科作业及其他自主学习)为![]() 小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到
小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到![]() );
);
(2)以统计的频率作为概率,估计一个高三备考学生每天完成数学作业的平均时间不超过![]() 分钟的概率.
分钟的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com