
【题目】已知函数![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
B.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
C.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
D.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
【答案】D
【解析】
利用周期函数的定义,通过取特值,结合二倍角公式求得![]() 最小正周期的可能的一系列的值,然后从小到大进行检验,得到函数
最小正周期的可能的一系列的值,然后从小到大进行检验,得到函数![]() 的最小正周期;利用二倍角的三角函数公式展开整理,再利用三角函数的性质和二次函数的性质判定
的最小正周期;利用二倍角的三角函数公式展开整理,再利用三角函数的性质和二次函数的性质判定![]() 单调性,进而作出判定.
单调性,进而作出判定.
设![]() 是
是![]() 的周期,则
的周期,则![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() 或
或![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,
当![]() 时,
时,![]()
![]() ),
),![]()
∴π不是![]() 的周期,
的周期,
若![]() ,则
,则![]() ,
,
当![]() 时,
时,![]()
![]() ),
),![]() ,
,
∴![]() 不是函数f(x)的周期,
不是函数f(x)的周期,
![]() ,则
,则![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
![]() ,∴
,∴![]() 不是函数f(x)的周期,
不是函数f(x)的周期,
![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 是
是![]() 的周期,
的周期,
∴![]() 是
是![]() 的最小正周期.
的最小正周期.
关于函数的单调性:
![]() ,
,
在![]() 上,
上,![]() 从0递增到1,再从1递减到0,
从0递增到1,再从1递减到0,![]() 从
从![]() 递增到
递增到![]() ,再递减到
,再递减到![]() ,
,
![]() 从
从![]() 递减到0,再从0递增到
递减到0,再从0递增到![]() ,再从
,再从![]() 递减到0,再从0递增到
递减到0,再从0递增到![]() ,
,
∴![]() 在
在![]() 上不是单调递增函数,
上不是单调递增函数,
在![]() 上,
上,![]() 从-1单调递增到
从-1单调递增到![]() ,
,![]() 从
从![]() 单调递增到0,
单调递增到0,
![]() 从
从![]() 单调递减到0,∴
单调递减到0,∴![]() 从-3单调递增到
从-3单调递增到![]() ,
,
综上所述,ABC错误,D正确.
故选:D.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:
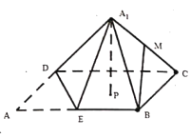
【题目】已知四边形![]() 为矩形,
为矩形,![]() ,E为
,E为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,连接
折起,连接![]() ,
,![]() ,得到四棱锥
,得到四棱锥![]() ,M为
,M为![]() 的中点,
的中点,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,在翻折过程中,下列四个命题正确的序号是________.
,在翻折过程中,下列四个命题正确的序号是________.
①![]() 平面
平面![]() ;
;
②三棱锥![]() 的体积最大值为
的体积最大值为![]() ;
;
③点M的轨迹是圆的一部分,且![]() ;
;
④一定存在某个位置,使![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系,过点
轴建立直角坐标系,过点![]() 作倾斜角为
作倾斜角为![]() (
(![]() )的直线
)的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 垂直,且与曲线
垂直,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是目前已知RNA病毒中基因组最大的一个病毒家族,可引起人和动物的呼吸系统、消化系统、神经系统等方面的严重疾病.自2019年底开始,一种新型冠状病毒COVID-19开始肆虐全球.人感染了新型冠状病毒后初期常见发热乏力、咽痛干咳、鼻塞流涕、腹痛腹泻等症状,严重者可致呼吸困难、脏器衰竭甚至死亡.筛查时可先通过血常规和肺部CT进行初步判断,若血液中白细胞、淋巴细胞有明显减少或肺部CT有可见明显磨玻璃影等病毒性肺炎感染症状则为疑似病例,可再通过核酸检测做最终判断,现A、B、C、D、E五人均出现了发热咳嗽等症状,且五人发病前14天因求学、出差、旅行、探亲等原因均有疫区旅居史.经过初次血液化验已确定其中有且仅有一人罹患新冠肺炎,其余四人只是普通流感,但因化验报告不慎遗失,现需要再次化验以确定五人中唯一患者的姓名,下面是两种化验方案:
方案甲:逐个化验,直到能确定患者为止;
方案乙:混合检验,先任取三人血样混合在一起化验,若混合血液化验结果呈阳性则表明患者在这3人中,然后再逐个化验,直到能确定患者为止;若混合血液化验结果呈阴性,则在另外2人中任选一人进行化验.假设在接受检验的血液样本中每份样本是阳性结果是等可能的,且每份样本的检验结果是阳性还是阴性都是相互独立的.
(1)求依方案甲所需化验次数![]() 不少于依方案乙所需化验次数
不少于依方案乙所需化验次数![]() 的概率;
的概率;
(2)求![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
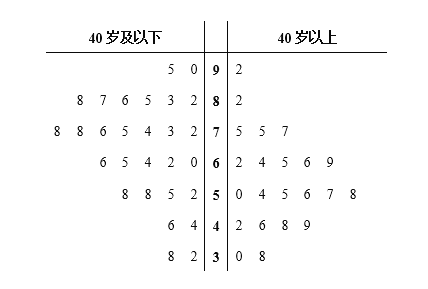
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: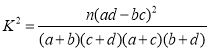 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com